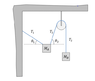
I'm getting 13.85 degrees.
The thing you need to remember is that diagrams such as the one you uploaded do not necessarily reflect the problem's eventual solution. Even though the diagram is drawn so it appears that ##\theta_2 > \theta_1##, there is no reason to assume that this is the case. This is a specific instance of a problem I've encountered many times--frequently, when I'm thinking about a complicated problem, I draw a diagram and begin to make assumptions and write equations based on it, only to realize later that I've inadvertently incorporated some of the "non-generic" features of the diagram into the math.
By the way, I always recommend writing your equations without using specific numbers at first, only substituting at the end of the problem. In this case it makes the solution much cleaner and easier to follow. Indeed, the equations for equilibrium are
$$M_A g = T_1 \sin (\theta_1) + T_2 \sin(\theta_2)$$ $$T_1 \cos(\theta_1) = T_2 \cos(\theta_2)$$ $$M_B g = T_2$$
Using the second equation to eliminate ##T_1## and the third to eliminate ##T_2##, and rearranging a bit, gives
$$\frac{M_A}{M_B} = \tan(\theta_1) \cos(\theta_2) + \sin(\theta_2)$$
Now, there are various ways of solving this equation, but the clearest seems to be doing what the problem suggests--using this to generate a quadratic equation for ##\tan(\theta_2)##. Let's clean up the notation a bit: Let ##r = M_A / M_B##, ##t = \tan(\theta_1)##, and ##T = \tan(\theta_2)##. Divide both sides by ##\cos(\theta_2)## and square:
$$r^2 \left( \frac{1}{\cos^2(\theta_2)} \right) = t^2 + 2tT + T^2$$
Finally, use the identity ##\cos^{-2}(\theta_2) = 1 + \tan(\theta_2)^2 = 1 + T^2## to get (again after rearranging)
$$(1 - r^2) T^2 + 2tT + (t^2 - r^2) = 0$$ which is the promised quadratic equation. Solving it gives the two solutions ##T \approx .246619## and ##T \approx -3.45412##, of which only the former is physical. Taking an inverse tangent gives ##\theta_2 \approx 13.85## degrees.