Finding Tension T1 in a Pulley System

[emilyb1995]

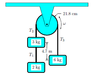
A pulley is massless and frictionless. The
masses 2 kg, 3 kg, and 6 kg are suspended as
in the figure.

(Figure Attached)

What is the tension T1 in the string be-
tween the two blocks on the left-hand side
of the pulley? The acceleration of gravity is
9.8 m/s2 .
Answer in units of N


I'm completely stupped and have no clue where to begin. Just a hint on where to begin would be appreciated.

 

[SHISHKABOB]

you should start by drawing a free-body diagram for each mass

 

[emilyb1995]

It would just be Fg and Ft acting on each mass, correct?

 

[SHISHKABOB]

well, yeah. The only forces here are the force of gravity on each mass and the force due to the strings on each of them

if you write down the net force for each of them then you should be able to see where to go from there

I write them down like this: (I'm going to tall the 6k mass m₁)

F₁ = m₁g - T₃

it's important to make sure the signs of each force are correct. I am setting downwards to be the positive direction.

(to get the little subscripts you can use the X₂ button in the second row of the list of buttons in the post editor thingy)

 

[emilyb1995]

Okay. So, if the 3kg mass is m₂ and the 2kg mass is m₃:

F₂=T₂-m₂g
and
F₃=T₁-m₃g

Are those correct?

Everything plugged in would be:

F₁=6a=58.8-T₃
F₂=3a=T₂-29.4
F₃=2a=T₁-19.6

 

[SHISHKABOB]

Okay. So, if the 3kg mass is m₂ and the 2kg mass is m₃:

F₂=T₂-m₂g
and
F₃=T₁-m₃g

Are those correct?

Everything plugged in would be:

F₁=6a=58.8-T₃
F₂=3a=T₂-29.4
F₃=2a=T₁-19.6

well, really, at this point you don't want to plug anything in just yet. Oftentimes I find it easier to go through a physics problem with just the variables; it makes things less complicated when I write it down, and I know exactly where everything is, in case I need to do some algebra to it. also, I would reexamine the forces acting on the 3kg mass, m₂

and then finally, of course, we're going to need the net force on the entire system, which is simply F_net = (m₁ + m₂ + m₃)a

 

[emilyb1995]

That makes sense. So, with the 3k force, would it be
F₂=T₂-(m₂g+m₃g) ?
And if so, how would I solve for T₁?

 

[SHISHKABOB]

That makes sense. So, with the 3k force, would it be
F₂=T₂-(m₂g+m₃g) ?
And if so, how would I solve for T₁?

Well, it's actually a bit simpler than that. If you just look at the 3kg mass, there should be three forces acting on it. You got gravity and the 2nd tension force, but there's one more.

 

[emilyb1995]

Would T₁ be acting on it as well?

 

[SHISHKABOB]

Would T₁ be acting on it as well?

yep, so now you have four equations, right? One for the force acting on each mass, and one for the net force on the system. Don't forget that the net force acting on any object or system is just the sum of the forces acting on it.

 

[emilyb1995]

Hmmm. You lost me. Would the system's Net Force equation just be m₁g-T₃+T₂-T₁-m₂g+T₁-m₃g

 

[SHISHKABOB]

Hmmm. You lost me. Would the system's Net Force equation just be m₁g-T₃+T₂-T₁-m₂g+T₁-m₃g

it's just F₁ + F₂ + F₃

those are the three forces acting on the system, so we just add them together to get the total. You should find that the tension forces all cancel out (pay close attention to how T₂ and T₃ relate to each other if you don't see why they cancel out).

 

[emilyb1995]

Because the masses are suspended, would F₂+F₃=F₁?

P.S. Sorry for all the questions, I'm having some trouble wrapping my head around it.

 

[SHISHKABOB]

That would be true if the system were not moving. However, one side of the pulley has more mass than the other side. Common sense tells us that the side with more mass will go downwards, while the side with less mass will move upwards. So we know that the total force on the system can't be zero, because the masses are unbalanced.

So, there are three parts to this system. And to get the sum of the forces acting on the system, you just add up all the forces acting on each part of the system.

We're doing this because we don't know the total acceleration of the system. We need that to figure out T₁. We know that all we need is a, because in the equation for F₃, the only unknown quantity besides T₁ is a.

it's m₃ = T₁ - m₃g

so by determining a, we can determine T₁ using that equation

to determine a, we need to find out what the total force acting on the system is. And since we have equations for each of the individual forces acting on the system we can just add them up to find the net force.

 

[emilyb1995]

Just clicked. Thank you so much. Got it right. :)