Luongo
- 119
- 0
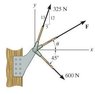
1. If the resultant force acting on the bracket is to be 790N directed along the positive x axis, determine the magnitude of F
2. Basically I got the components of the two vectors above and below F summed them up. I got THE RESULTANT X-component: 600cos45+325(5/13)+790cos(theta)
3. Same with the y component of the resultant HOW DO I GET THETA? I can't get the magnitude of F which is sqrt(Frx^2+Fry^2) without knowing that angle between x-axis and F. Does anyone know how to get that angle and what i do? Thanks!
2. Basically I got the components of the two vectors above and below F summed them up. I got THE RESULTANT X-component: 600cos45+325(5/13)+790cos(theta)
3. Same with the y component of the resultant HOW DO I GET THETA? I can't get the magnitude of F which is sqrt(Frx^2+Fry^2) without knowing that angle between x-axis and F. Does anyone know how to get that angle and what i do? Thanks!