Finding the coefficient of restitution

[Saitama]

Homework Statement

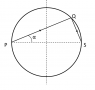
A body is fired from point P and strikes at Q inside a smooth circular wall as shown in figure. It rebounds to point S (diametrically opposite to P). The coefficient of restitution will be:

(Ans: $\tan^2\alpha$)

Homework Equations

The Attempt at a Solution

Let $v$ (along PQ) be the velocity before collision and $v'$ (along QS) be the velocity after collision.

The coefficient of restitution (e) is defined as:
$$e=\frac{\text{Relative speed after collision}}{\text{Relative speed before collision}}$$

The numerator is $v'\sin\alpha$ and denominator is $v\cos\alpha$. (The relative speed is measured along normal at the point of collision)

Hence,
$$e=\frac{v'\sin\alpha}{v\cos\alpha}=\frac{v'}{v}\tan\alpha$$

From conservation of linear momentum along PS:
$$mv\cos\alpha=mv'\sin\alpha \Rightarrow \frac{v'}{v}=\cot\alpha$$
Hence,
$$e=1$$


Any help is appreciated. Thanks!

 

[TSny]

From conservation of linear momentum along PS:

Why would this be true? Notice that the problem says that the surface of the wall is smooth.

 

[Saitama]

Notice that the problem says that the surface of the wall is smooth.

Yes but I don't see how it has got anything to do with conservation of momentum.

 

[TSny]

"Smooth" means that the wall will not exert any tangential component of force on the body.

 

[Saitama]

"Smooth" means that the wall will not exert any tangential component of force on the body.

Why are we talking about the tangential force now? Had it been present, does it mean that momentum would be conserved?

 

[TSny]

If there is no force on a body in a certain direction, what does that mean about the component of momentum of the body in that direction?

 

[Saitama]

If there is no force on a body in a certain direction, what does that mean about the component of momentum of the body in that direction?

The momentum is conserved in that direction.

Do you mean I should conserve momentum in radial direction?

 

[TSny]

The momentum is conserved in that direction.

Yes. So, smooth means that the tangential component of momentum will be conserved. That is, the component of momentum parallel to the wall at the point of collision will be conserved.

Note that PS is not the tangential direction.

Do you mean I should conserve momentum in radial direction?

No, the tangential component (parallel to the wall) is conserved.

 

[Saitama]

Yes. So, smooth means that the tangential component of momentum will be conserved. That is, the component of momentum parallel to the wall at the point of collision will be conserved.

Thanks TSny!

This time I get, $v\sin\alpha=v'\cos\alpha$ which gives the right answer.

 

[Swesha]

Thanks TSny!

This time I get, $v\sin\alpha=v'\cos\alpha$ which gives the right answer.[/QUOTE

Thanks TSny!

This time I get, $v\sin\alpha=v'\cos\alpha$ which gives the right answer.

How do you get this relation? Can you please explain further?

 

[TSny]

@Swesha
See post #8

 

[Swesha]

@Swesha
See post #8

Okay. Thanks :) @TSny