Saitama
- 4,244
- 93
Homework Statement
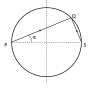
A body is fired from point P and strikes at Q inside a smooth circular wall as shown in figure. It rebounds to point S (diametrically opposite to P). The coefficient of restitution will be:
(Ans: ##\tan^2\alpha##)
Homework Equations
The Attempt at a Solution
Let ##v## (along PQ) be the velocity before collision and ##v'## (along QS) be the velocity after collision.
The coefficient of restitution (e) is defined as:
$$e=\frac{\text{Relative speed after collision}}{\text{Relative speed before collision}}$$
The numerator is ##v'\sin\alpha## and denominator is ##v\cos\alpha##. (The relative speed is measured along normal at the point of collision)
Hence,
$$e=\frac{v'\sin\alpha}{v\cos\alpha}=\frac{v'}{v}\tan\alpha$$
From conservation of linear momentum along PS:
$$mv\cos\alpha=mv'\sin\alpha \Rightarrow \frac{v'}{v}=\cot\alpha$$
Hence,
$$e=1$$
Any help is appreciated. Thanks!