jisbon
- 475
- 30
- Homework Statement
- An object is located 20cm to the left of a concave mirror (with curvature 10cm). Light leaves object is the first incident on the mirror and passes through the lens of 10cm in focal length located left of the object. A final image formed by the system is located a the same location as the original object.
i) Find distance between lens and mirror
ii) Comment on orientation and magnification of the final image
- Relevant Equations
- ##\dfrac {1}{p}+\dfrac {1}{q}=\dfrac {1}{f}##
Hi all,
Pretty new to optics here, so would like to get my basics right.
Below is my working, was wondering if my concepts are correct here.
First I will separate mirror and lens and solve them 1 by 1, so solving for mirror first,
##\dfrac {1}{p_{1}}+\dfrac {1}{q_{1}}=\dfrac {1}{f_{1}} ## where ##p_{1}## is the object distance to mirror and ##q_{1}## is the image distance to mirror.
Putting ##p_{1}## as 20cm and ##{f_{1}}## as 5cm (since f=R/2) , I get ##q_{1}## to be 20/3 cm
From what I understand, since ##q_{1}## is positive, this means it is infront of the mirror, so it should be something like:
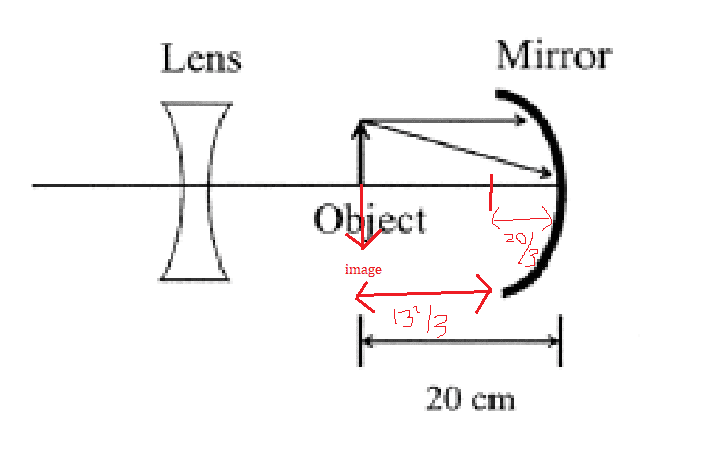
this?
Assuming this is correct,
Now moving on to the lens,
##\dfrac {1}{p_{2}}+\dfrac {1}{q_{2}}=\dfrac {1}{f_{2}} ##
let x be the distance between between object and lens,
so from the above equation,
Taking ##p_{2}## = distance between object and lens
and
##q_{2}## = distance between image and lens
##\dfrac {1}{p_{2}}+\dfrac {1}{q_{2}}=\dfrac {1}{f_{2}} ##
where the new object is the image projected by the mirror,
##\dfrac {1}{x+13.333}+\dfrac {1}{x}=\dfrac {1}{-10} ##
and from here I can find x where (i) will be x +20cm
Is this correct? Thanks
Pretty new to optics here, so would like to get my basics right.
Below is my working, was wondering if my concepts are correct here.
First I will separate mirror and lens and solve them 1 by 1, so solving for mirror first,
##\dfrac {1}{p_{1}}+\dfrac {1}{q_{1}}=\dfrac {1}{f_{1}} ## where ##p_{1}## is the object distance to mirror and ##q_{1}## is the image distance to mirror.
Putting ##p_{1}## as 20cm and ##{f_{1}}## as 5cm (since f=R/2) , I get ##q_{1}## to be 20/3 cm
From what I understand, since ##q_{1}## is positive, this means it is infront of the mirror, so it should be something like:
this?
Assuming this is correct,
Now moving on to the lens,
##\dfrac {1}{p_{2}}+\dfrac {1}{q_{2}}=\dfrac {1}{f_{2}} ##
let x be the distance between between object and lens,
so from the above equation,
Taking ##p_{2}## = distance between object and lens
and
##q_{2}## = distance between image and lens
##\dfrac {1}{p_{2}}+\dfrac {1}{q_{2}}=\dfrac {1}{f_{2}} ##
where the new object is the image projected by the mirror,
##\dfrac {1}{x+13.333}+\dfrac {1}{x}=\dfrac {1}{-10} ##
and from here I can find x where (i) will be x +20cm
Is this correct? Thanks