- #1
Karma1
- 3
- 0
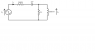
The frequency, ω, of the source in the circuit of Figure 2 is adjusted until ig is in phase with vg.
(a)using complex notation, determine the value of ω (rad/sec)
Can anyone out there please help with this question? I've tried multiple methods but I am really struggling with simplifying the equation and my answers are wildly inaccurate.
(Please see attached document for details of the circuit)
(a)using complex notation, determine the value of ω (rad/sec)
Can anyone out there please help with this question? I've tried multiple methods but I am really struggling with simplifying the equation and my answers are wildly inaccurate.
(Please see attached document for details of the circuit)