NHLspl09
- 96
- 0
As previously stated in other threads, I have started to work on a summer assignment for my Fall semester EE course. I was given a circuit and asked to derive an expression for the gain (Attachment 1). I have not yet started to write out the problem on paper, but have two thoughts as to where I need to begin based on referencing an EE book I've had from previous courses (Attachment 2). Right now all I'm asking for is some input on whether my thoughts are correct about where I should begin, or I'm just making things up. Any input would be much appreciated!
(Attachment 1)
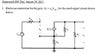
Derive an expression for the gain of the small-signal circuit shown.
Ok so with looking at the book, it seems to be I need to begin on the right hand side of the circuit for this problem. Now my two thoughts are:
Homework Statement
(Attachment 1)
Derive an expression for the gain of the small-signal circuit shown.
Homework Equations
The Attempt at a Solution
Ok so with looking at the book, it seems to be I need to begin on the right hand side of the circuit for this problem. Now my two thoughts are:
- ro and Rs are in parallel/series, which the result is then in parallel with RL
- ro and RL are in parallel



 I see now though, thanks for the clarification!
I see now though, thanks for the clarification!