SUMMARY
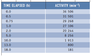
The discussion centers on the calculation of half-life from a given activity table. The user initially calculated a half-life of 2.34 minutes by halving the initial activity of 36506, which was incorrect. The correct half-life, as stated in the textbook, is 1 minute. The confusion arose from misinterpreting the relationship between activity decay and time, leading to an erroneous conclusion regarding the duration of the half-life.
PREREQUISITES
- Understanding of radioactive decay principles
- Familiarity with half-life calculations
- Basic knowledge of activity measurement in nuclear physics
- Ability to interpret data tables
NEXT STEPS
- Study the concept of radioactive decay and its mathematical models
- Learn how to accurately calculate half-life from activity data
- Explore the relationship between activity and time in decay processes
- Review examples of half-life calculations in nuclear chemistry
USEFUL FOR
This discussion is beneficial for students in nuclear physics, researchers in radiochemistry, and anyone involved in calculating half-lives in scientific contexts.