fresh_42 said:
I tried this and ended up with circle equations: x+1=p=r⋅cosφ,s=r⋅sinφ.
haruspex said:
Or some other family, e.g. circles radius r centred at (r-1,0), 0<r<1.
The issue may be that our domain is the unit disk defined as {x
2 + y
2 <1} and taking from a different subset of the xy-plane such as an offset disc will map to different points on the uv- plane.
Infrared said:
I think the image should be the right half plane u>0. This mapping looks like the usual conformal equivalence from the disk to the half plane in C written out in cartesian coordinates (I didn't check this though).
Anyway it should be clear that the u coordinate of any point in the image can be any positive number, so try to show for fixed u that you can also make v arbitrary. I think you can either do this directly or with the trig arguments suggested above. If you work out what this function is as a holomorphic map, you can probably even write down an inverse.
It seems that the image does not fill the right half-plane. An arbitrary point (u,v) corresponds to a point (x,y) and our map does not allow v to be arbitrary with respect to u, or vice versa.
Is holomorphic mapping a complex analysis technique? It is beyond my experience or knowledge at the moment.
Here is a graph I have been staring at for a few days. It is a graph of the equations in our map, and it is only a representation of it, or a way to visualize it. Since we can only work in three dimensions, we substitute u and v with z and use the two colors to establish the fourth dimension. In this graph, each pair of the z coordinates of the two surfaces correspond to a point (u, v) on the uv plane. We choose the point (u,v) by looking at the points on the surfaces above a single point (x, y) (taken from the unit disc, because it is our domain), take their z coordinates and and map them mentally in the uv plane. We observe the singularities at the point (x, y) = (-1, 0). This graph tells us everything about the image except for the asymptotic behavior.
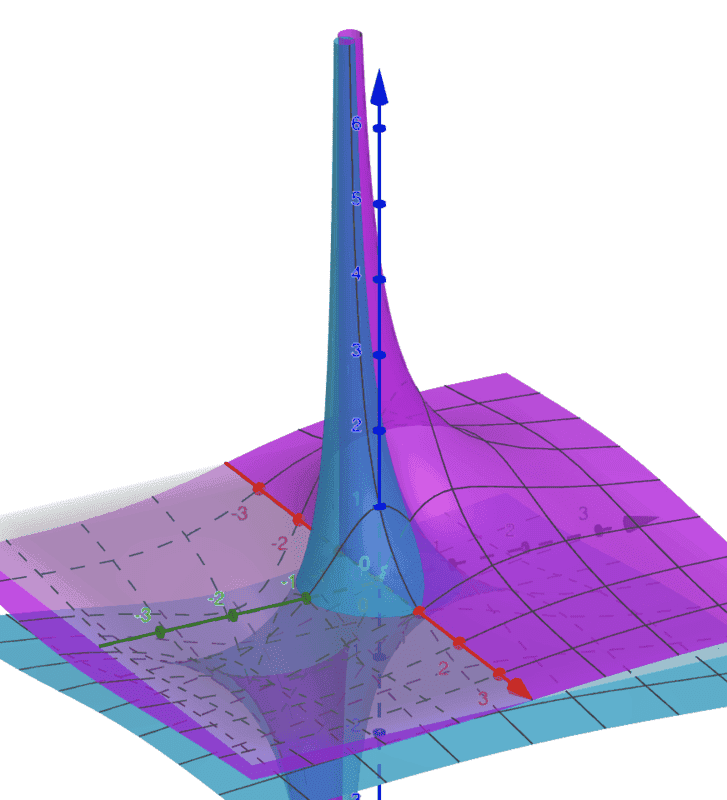
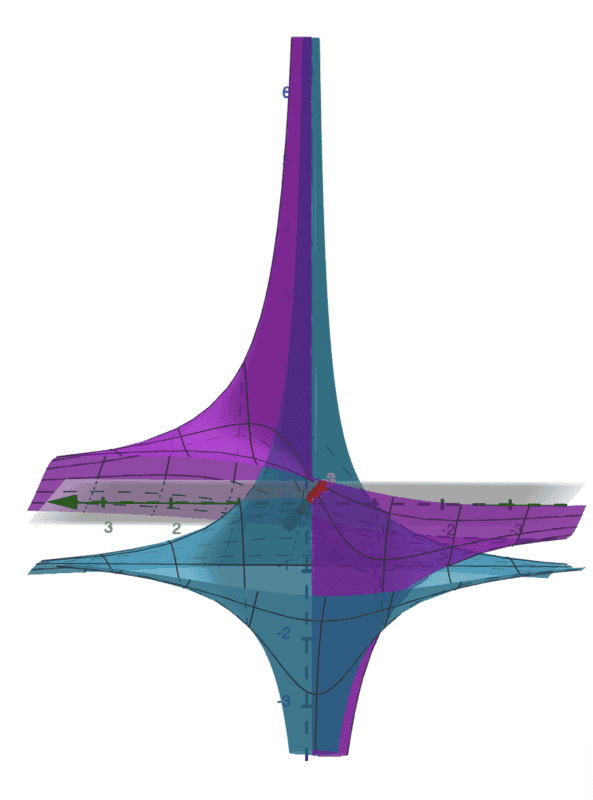
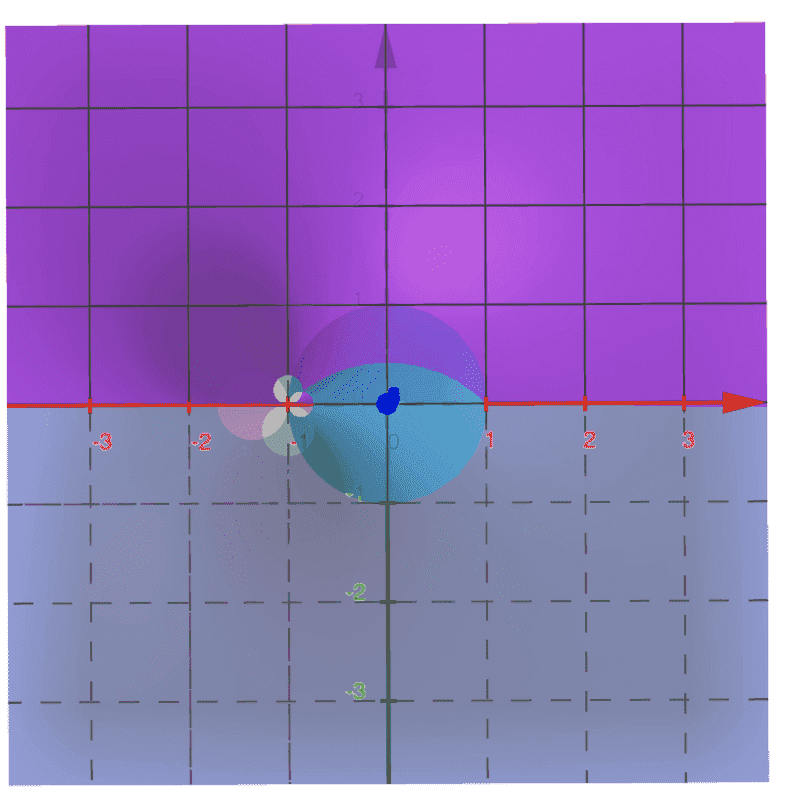
I also re-visited the concentric circles method. As we observed earlier, finding the curves in the UV plane as implicit equations in Θ is difficult. We try to do this by using trigonometric substitutions for u and v and solve for Θ, and set them equal to each other to get rid of Θ. Let r = .5
From the equation u, we have the following. (ignore the 2pi n term, as it does not matter to us).
Θ =
From the equation v, here is what we have for Θ (replace x with Θ).
So the implicit equation for the curve {r=.5} under our map is the equality between these two expressions.