Trap_Shooter
- 1
- 0
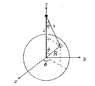
Three point charges are placed at the vertices of an equilateral triangle (of side .2m). The triangle is setup on an X-Y plain. On the top of the triangle on the Y-axis the charge is q7= -7μC, the positive X-axis the charge is q3= 3μC, and on the -X-axis the charge is q2= 2μC.
Part A).
What is the magnitude and the direction of the electric field at the origin?
Part B).
What would be the acceleration (magnitude and direction) of an electron placed at the origin?
Part C).
Would the acceleration (magnitude and direction) of the proton be different than that of the electron? Explain.
Part A).
What is the magnitude and the direction of the electric field at the origin?
Part B).
What would be the acceleration (magnitude and direction) of an electron placed at the origin?
Part C).
Would the acceleration (magnitude and direction) of the proton be different than that of the electron? Explain.