Underhill said:
Thanks, gneill.
(i.) is easy. The energy stored in a partially charged capacitor is \stackrel{1}{2}QV
In our case, we get \stackrel{1}{2}(.105)(9.0) = 0.4725 Joules
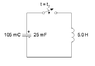
Um, how did you decide that the voltage on the capacitor is 9.0V when it has a charge of 105 mC? Remember that even though the original circuit had a 9V source, the switch was operated before charging completed, giving the capacitor just 105 mC of charge.
So what's the actual starting voltage on the capacitor for times t2
+?
(ii.) is harder. The total energy we have to work (or play) with is the amount of energy stored in the capacitor at time t2, which is 0.4725 Joules. The energy stored in the magnetic field of an inductor is -\stackrel{1}{2}LI2. (By the way, I'm not sure how relevant the minus sign is here. I think it has to do with Lenz's Law, but don't know if it makes sense in this context. Can you explain?)
The negative sign won't matter here as we only need to deal with the magnitude of the energy.
When a circuit oscillates the energy is shuttled back and forth between storage components. In an undamped circuit, at certain instants of time ALL of the energy will be in one component, at other instants it will all be stored in the other component.
Our story begins with all of the energy crammed into the capacitor; No current is flowing in the inductor so there is no magnetic field (inductors store energy in their magnetic fields).
A half cycle of oscillation later and we can expect all the energy stored in the capacitor to have been shuttled over to the inductor. It will then have ALL the energy, stored in its magnetic field tied to the current flowing through it. Current will be maximum at that instant.
So setting this expression equal to 0.4725 Joules, the total energy in the circuit, and substituting in L = 5.0 Henri's, we have
0.4725 = \stackrel{1}{2}(5.0)(I2)
I ≈ 0.4347 Amps
Fix your energy calculation to reflect the actual starting voltage on the capacitor and you'll be able to calculate the correct maximum current.
(iii.) I'm not sure what to do here. It looks like I need to take the derivative of something, but I'm not sure where to begin. What do you mean by natural frequency? I didn't study this in high school. Could you quickly brief me on the natural frequency of oscillating LC circuits?
If you have the maximum current and voltage and charge values and you know that the circuit oscillates. You can therefore write equations for the current, voltage, charge, with respect to time. All you need is the
natural frequency of the oscillations. Look up "LC circuit" "natural frequency".
Maximum voltage or electric potential appears to be the same 9.0V as was present before the switch was flipped. Does this make sense?
Nope, as I explained above