Finding the period T for cylinder on spring

[jjr]

Hi,
the problem isn't written in English originally, so there might be some slight mixing up in the terminology


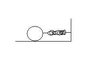
A cylinder with mass M = 2 kg is attached to a spring and lying on a horizontal plane. (Imagine looking at it from the side, with the wall where the spring is attached forming a 90 angle with the plane. The spring extends to the cylinder, which will look like a circle from our point of view (we're looking straight through the cylinder axis))
The spring has a stiffness of k = 30 N/m. The cylinder is pulled slightly out from the equilibrium position and is then let go. It's rolling back and forth without slipping. What's the period T?
(No friction involved here)

Seemed pretty straightforward to me: We have the angular velocity (I think it's called) which is ω = \sqrt{k/M}. The period is given by T = \frac{2∏}{ω}
Values go in and voila: \frac{2∏}{3.87} = 1.62 seconds. Problem is the solution set says 1.99 seconds!

Any suggestions? Does it have something to do with the relevant object being a non-slipping cylinder?

Thanks, J

 

[kushan]

can u draw the figure please :)

 

[jjr]

Here's my best shot!

 

[SHISHKABOB]

I'm a little bit confused as to how a spring causes the cylinder to roll, but I think that's the idea of what they're trying to do. I think that the increased period length comes from the fact that the cylinder is rolling instead of just sliding across the ground.

EDIT: Oh, I guess it's attached to it like an axle.

 

[Screwdriver]

You can't just assume that \omega = \sqrt{k/M}. This would be true if the mass was just sliding with no friction, but it will also have some rotational energy since it's a cylinder.

I would proceed by writing down the total energy in terms of the angle \theta of displacement, and then taking the derivative with respect to time.

 

[kushan]

Yea , and don't forget to take MOI about the Surface .

 

[kushan]

what is the answer given?

 

[SHISHKABOB]

what is the answer given?

in his OP he says it should be 1.99 seconds for the period

 

[ehild]

Take care, there are two ω-s. The CM of the cylinder performs simple harmonic motion connected with the spring with an angular frequency Ω while the cylinder itself rolls with angular speed ω(t). During pure rolling, the translational velocity of the CM and the angular velocity of the rotation are related as v=rω, and the same relation holds for the translational and angular accelerations.

Write out the equation torque=moment of inertia x angular acceleration for the instantaneous axis of rotation, the line of contact between cylinder and the ground.


ehild