Finding the Ratio of Dimensions for Equal Hydrostatic Force on a Vertical Plate

[dhkdeoen]

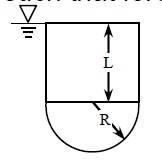
1. A vertical plate consists of rectangular and semicircular portion and has dimensions as shown. It is submerged in a liquid such that the upper edge coincides with the free surface of the liquid. What is the ratio of L/R such that force on the rectangular portion is the same as that on the circular portion?

Homework Equations

F=γhA

The Attempt at a Solution

For rectangular part, since height of it is L and width of it is 2R
A=2R*L
h=L/2
so force on retangular part is
F_r=γ*2RL*L/2=γRL²

for semi circular portion
h=L+4R/3∏
A=∏R²/2
∴F_sc=γ(L+4R/3∏)*∏R²/2

Since F_r=F_sc

2RL²=(L+4R/3∏)∏R²(γ canceled out)
.
.
L²=∏RL/2+2/3R²

now I'm stuck here. Am I doing this right? or did I misunderstand the problem?

English isn't my first language, so bear me.

 

[BvU]

You're doing just fine. Remember you want an answer for L/R, so if you call that x, all you have to do is rewrite the last equation to get something with x and a few numbers...

 

[haruspex]

Looks good so far. How can you turn this into an equation only involving the ratio L/R? How do you solve a quadratic?

 

[dhkdeoen]

so..

er.. so I divide both side with R^2

(L/R)^2=pi*L/(2R)+2/3

since L/R=x

x^2=pi/2x+2/3
x^2-pi/2x-2/3=0

and this gives me two roots

x1=1/12(3pi-sqrt(96+9pi^2)=-0.3475...
x2=1/12(3pi+sqrt(96+9pi^2)=1.91832..

so I pick the one bigger than 0; which is x2.

so L/R should be 1.91832, right?

 

[haruspex]

er.. so I divide both side with R^2

(L/R)^2=pi*L/(2R)+2/3

since L/R=x

x^2=pi/2x+2/3
x^2-pi/2x-2/3=0

and this gives me two roots

x1=1/12(3pi-sqrt(96+9pi^2)=-0.3475...
x2=1/12(3pi+sqrt(96+9pi^2)=1.91832..

so I pick the one bigger than 0; which is x2.

so L/R should be 1.91832, right?

Looks right, but I would tend to give the answer in surd form, not reduce it to a numerical approximation.

 

[dhkdeoen]

whoa.. it is hard to get back to old thread. Thanks!