dhkdeoen
- 11
- 0
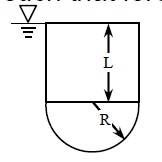
1. A vertical plate consists of rectangular and semicircular portion and has dimensions as shown. It is submerged in a liquid such that the upper edge coincides with the free surface of the liquid. What is the ratio of L/R such that force on the rectangular portion is the same as that on the circular portion?
F=γhA
For rectangular part, since height of it is L and width of it is 2R
A=2R*L
h=L/2
so force on retangular part is
Fr=γ*2RL*L/2=γRL2
for semi circular portion
h=L+4R/3∏
A=∏R2/2
∴Fsc=γ(L+4R/3∏)*∏R2/2
Since Fr=Fsc
2RL2=(L+4R/3∏)∏R2(γ canceled out)
.
.
L2=∏RL/2+2/3R2
now I'm stuck here. Am I doing this right? or did I misunderstand the problem?
English isn't my first language, so bear me.
Homework Equations
F=γhA
The Attempt at a Solution
For rectangular part, since height of it is L and width of it is 2R
A=2R*L
h=L/2
so force on retangular part is
Fr=γ*2RL*L/2=γRL2
for semi circular portion
h=L+4R/3∏
A=∏R2/2
∴Fsc=γ(L+4R/3∏)*∏R2/2
Since Fr=Fsc
2RL2=(L+4R/3∏)∏R2(γ canceled out)
.
.
L2=∏RL/2+2/3R2
now I'm stuck here. Am I doing this right? or did I misunderstand the problem?
English isn't my first language, so bear me.