umzung
- 21
- 0
- Homework Statement
- Calculate:
- Relevant Equations
- The sum of 5 x 10^i, from i=0 to i=n-1
I'm using the sum of a geometric series formula, but I'm not sure how to find the ratio, r. The n is confusing me.
The solution is below, but I'm having trouble with the penultimate step.
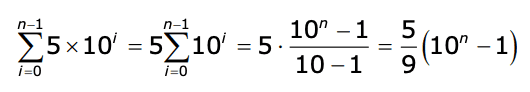
The solution is below, but I'm having trouble with the penultimate step.