Finding the Uncertainty in the motion of a pendulum

[aatari]

Homework Statement

What is the expression for the uncertainty in finding from the motion of a pendulum
g = 4π^2 L/T^2

Assuming an uncertainty in L of δL, and uncertainty in T of δT.

Relevant Equations

g = 4π^2 L/T^2

Hi guys can someone look at my work for uncertainty and let me know if it makes sense.

 

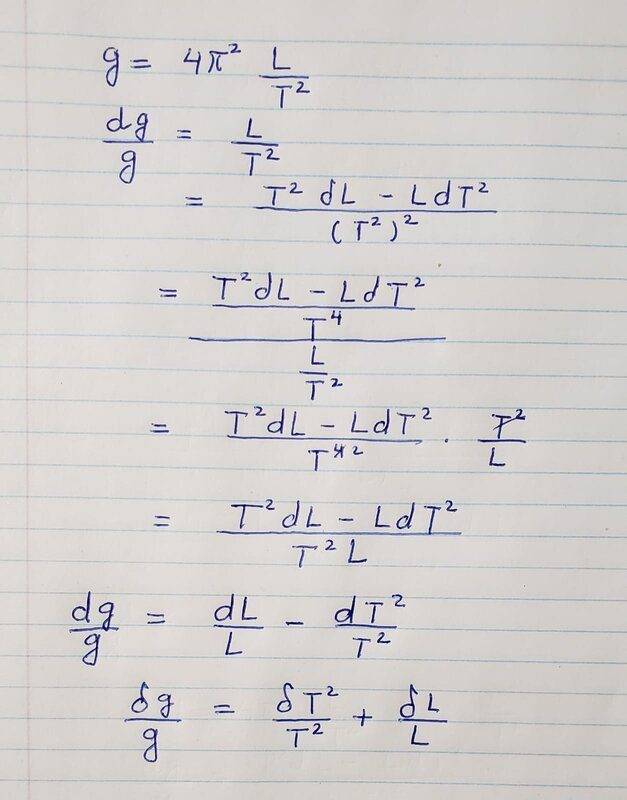
[BvU]

I don't even understand the first step. Where did you find that ?
Nor do I understand the last step. What are you doing there ?

What is the general formula for the (infinitesimal) variation in a function of two variables $f(x,y)$ in terms of the (infinitesimal) variation in $x$ and $y$ ?

 

[BvU]

Are you still there ?

 

[aatari]

sorry just seeing your message now. Actually the question asked to show the expression of uncertainty. I asked the TA and this is apparently correct based on the method in the attached image.

 

[BvU]

What is the general formula for the (infinitesimal) variation in a function of two variables f(x,y) in terms of the (infinitesimal) variation in $x$ and $y$ ?

My hunch is that this question and your

refer to one and the same:

For a function of one variable we write (casually) $$ {df\over dx} = f'\ \Rightarrow \ df = f'\, dx $$ or (for small $\Delta x$) : $$\Delta f \approx f'\,\Delta x$$

In the case of two variables this becomes $$df = {\partial f\over \partial x} dx + {\partial f\over \partial y} dy$$leading to (C.14) in your image for the case $f = {x\over y}$.

In your post #1, however, you write $$ g = 4\pi^2\, {L\over T^2} $$$$ {dg\over g} = {L\over T^2}$$which is something else and simply wrong (effectively, it says $g = 4\pi^2$ )

Could it be you meant $$ {dg\over g} = { d\,{L\over T^2} \over {L\over T^2}}\quad ? $$

I suggest you go a step back to the general formula and work out $\partial g\over \partial L$ and $\partial g\over \partial T$ to come to an expression for $dg$.

Once you fully understand that, we can work out an alternative approach using C.4 (and, as I suppose C.3).

 

[aatari]

My hunch is that this question and your View attachment 272252 refer to one and the same:

For a function of one variable we write (casually) $$ {df\over dx} = f'\ \Rightarrow \ df = f'\, dx $$ or (for small $\Delta x$) : $$\Delta f \approx f'\,\Delta x$$

In the case of two variables this becomes $$df = {\partial f\over \partial x} dx + {\partial f\over \partial y} dy$$leading to (C.14) in your image for the case $f = {x\over y}$.

In your post #1, however, you write $$ g = 4\pi^2\, {L\over T^2} $$$$ {dg\over g} = {L\over T^2}$$which is something else and simply wrong (effectively, it says $g = 4\pi^2$ )

Could it be you meant $$ {dg\over g} = { d\,{L\over T^2} \over {L\over T^2}}\quad ? $$

I suggest you go a step back to the general formula and work out $\partial g\over \partial L$ and $\partial g\over \partial T$ to come to an expression for $dg$.

Once you fully understand that, we can work out an alternative approach using C.4 (and, as I suppose C.3).

Thanks for your suggestion!