Finding the Volume Inside Two 3D Surfaces Using Integration Techniques

[bossman27]

Homework Statement

Find the volume of the solid inside the surfaces x^2+y^2+z^2=1 and z=x^2+y^2

Homework Equations

With x=0:
z=y^2 ; z=√(1-y^2)
or y as a function of z then gives:
y=√z ; y=√(z^2-1)

The Attempt at a Solution

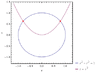
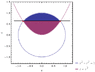
First, I attempted to sketch a cross section of the region by setting x=0 (y=0 would give a similar cross section), and graphing z=y^2and z=√(1-y^2) on the y-z plane.
This gives me a picture of a cross section of the region with Area=∫√(1-y^2)-y[^2]...
The problem is that I won't have a calculator to solve this type of problem and I can't figure out how to solve for the limits of integration... I set the z's equal and have:
y^4+y^2-1=0 but I don't know how to solve that for y by hand, and I'd have a similar problem if I solved for y and set the functions of z equal.

Because the solid is symmetrical about the z-axis, I know I could also solve for the volume by using V=∫∏(radius)^2.dz where radius is y(z)≥0, or distance from the z axis to the nearest of the two positive z(y) equations [from z=0 to z=1], but wouldn't I still need to solve for the intersection point of the two curves where y>0 to split the volume into two halves?

If I could solve for the intersection in terms of z, call it z0, I could solve
V=∫[0,z0] ∏(+√(z))^2.dz + ∫[z0,1] ∏(+√(z^2-1))^2.dz ... but again, I don't know what z0 would be, or how to find it without a calculator.

Apologies for not using Latex, I don't really know how to work it yet.

Edit: Or is there a way to convert to polar and solve?

 

[DryRun]

When finding the volume, it's a good practice to draw the graph, so you can better visualize the problem.

x^2+y^2+z^2=1 is a sphere with center origin and radius 1, and z=x^2+y^2 is a paraboloid.

This is an interesting problem. You will need to find the volume as the sum of two triple integrals.

The two sections of the volume are divided by the plane z=\frac{-1+\sqrt 5}{2}. So, you have to find the volume below and above that plane, separately, and add them up to get the whole volume of the solid.

I have attached the xz-trace coordinates (in the plane y=0) so you can understand the limits. The yz-trace coordinates look the same. I've also attached an edited graph of the same, showing the 2 sections of volume that you need to find. Note that the vertex of the parabola is the origin.

To make it easier, you can use cylindrical coordinates to find the lower region and spherical coordinates for the upper region.

 

[bossman27]

I did draw the graphs, both 3D and cross sectional.
I just figured out that I could solve for z by substituting the second equation into the first and getting z+z²=1... then using the quadratic formula I got z0=\frac{√5-1}{2}


For volume by rotation around z-axis I have r=√z and r=√(z^2-1) , and V=\int∏(radius)^2dz so:
I used V=∏\int(z)dz [0,\frac{√5-1}{2}] + ∏\int z^2-1dz [\frac{√5-1}{2},1]

Solving this gives me an answer of V= ∏(\frac{62}{24}- \frac{26√5}{24}) ≈ .5056

I forget if there's something special I need to do since both y(z) equations have a negative and positive solution for y(z0), and I only want the area above the z-axis... Did I forget something or does what I did look right?

Edit: woops, just realized I did the quadratic formula wrong... corrected now though.

 

[DryRun]

Using cylindrical coordinates to find the lower region of volume:
\int^{\theta = 2\pi}_{\theta = 0} \int^{r=0.786}_{r=0} \int^{z=\frac{-1+\sqrt 5}{2}}_{z=0} \,rdrd\theta dz
Now, using spherical coordinates to find the upper region of volume:
\int^{\theta=2\pi}_{\theta=0} \int^{\phi = 1.09}_{\phi = 0} \int^{\rho = 1}_{\rho = {0.618\sec \phi}} \, \rho ^2 \sin \phi d\rho d\phi d\theta
Evaluate both, and add them up to get the final volume of the solid.

Note: I have left out all the obvious calculations, as you should show your work. Use the triple integrals above as a guide to understand the limits of the 2 regions of volume. Without you showing any graphs, and not mentioning what coordinate system/s you used, it's difficult to explain where you went wrong in your understanding.

z=\frac{-1+\sqrt 5}{2}=0.618
x^2+y^2=0.618
r=\sqrt{0.618}=0.786

 

[bossman27]

I corrected the mistaken limit in the above post so after half a page of scribbling fractions I have a different final answer... although it does seem like too small of a volume.

I also tried working your triple integrals, although we never got past double integrals in polar in lecture so I would hope there's a way to solve it without needing the triples.

After a page of scribbling I came out with
Lower volume \frac{3∏-√5∏}{2√2} ≈ .848
Upper volume \frac{2∏√6}{9} ≈ 1.71007
This doesn't look like it makes sense as the lower volume should be great than the upper volume... probably an integration mistake on my part.

In any case, thanks for all the help, it's very much appreciated.

 

[LCKurtz]

There is no need to work this problem in two parts, nor any need to use spherical coordinates. $z$ on the lower surface is $z=r^2$ and $z$ on the upper surface is $z=\sqrt{1-r^2}$.$$
V=\int_0^{2\pi}\int_0^{\sqrt{\frac{-1+\sqrt 5} 2}}\int_{r^2}^{\sqrt{1-r^2}}r\, dz dr d\theta$$

Edit: Corrected upper limit for $r$, accidentally left off the square root.

 

[DryRun]

Just to clarify:
V=\int_{\theta=0}^{\theta=2\pi}\int_{r=0}^{r=\frac{-1+\sqrt 5} 2}\int_{z=r^2}^{z=\sqrt{1-r^2}}r\, dz dr d\theta
In that case, your limits don't make sense to me. The upper limit for r should be:
\sqrt { \frac {-1+\sqrt 5}{2} }
It's a very nice way of seeing the problem though.

 

[bossman27]

There is no need to work this problem in two parts, nor any need to use spherical coordinates. $z$ on the lower surface is $z=r^2$ and $z$ on the upper surface is $z=\sqrt{1-r^2}$.$$
V=\int_0^{2\pi}\int_0^{\frac{-1+\sqrt 5} 2}\int_{r^2}^{\sqrt{1-r^2}}r\, dz dr d\theta$$

This looks a lot easier, a more along the lines of what I was thinking...

However I was about to post the same thing as sharks. The upper limit of r is the y coordinate of the intersection, not the z coordinate.

Thanks to both of you guys, though. It's been a big help.

 

[LCKurtz]

The upper limit for r should be:
\sqrt { \frac {-1+\sqrt 5}{2} }

Yes. Corrected.