Sorin2225
- 20
- 1
- Homework Statement
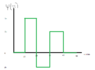
- I was given a probability density graph and from it I had to figure out what B was in nm^-1/2
- Relevant Equations
- I think it's just from the graph.
I assumed to find it I would need to find the area under the graph. I also assumed that the part under x would cancel out so I would be left with 2b*10=1 if it was, in fact, true that it had to equal to one. So my final answer was (1/10)/2 nm^-1 but the actual answer was 0.0845 nm^-1/2 and I'm unsure of how this answer was gained.