Finding velocity components of point in the middle of a tricycle

[Krus]

Homework Statement

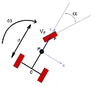
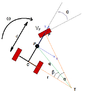
I have a tricycle with a following data (see attachment):

• Distance (d) between center of front wheel (F) and center between rear wheels (C) = 325 mm
  
• Velocity of front wheel (V_F) = 50 mm/s
• Angle of front wheel (α) = changing between -90;90
• Distance between point C and P = 129 mm

Out of this data, I calculated the angular velocity by using the following formula:
ω = (sin(α) * vF) / d

What I need, is the component velocity of a point between the front wheel and the center between rear wheels (P) in its local coordinate system. This local coordinate system is for sure turning with the vehicle.

Homework Equations

The Attempt at a Solution

To calculate the velocity in point P i used the angular velocity and the distance between C and P:

vP = ω * 129 mm

This is for sure right, if α = ±90. But If α = 0, my vP is also 0, which can't be.
So somehow the velocity connected with the front wheel angle α must have an influence as well.

Finally, I need to split the velocity of point P into its X- and Y-component.

Thanks for your help.
Krus

 

[BvU]

Hello Krus, and welcome to PF.

Your problem statement

What I need, is the component velocity of a point between the front wheel and the center between rear wheels (P) in its local coordinate system. This local coordinate system is for sure turning with the vehicle.

surprises me. In the local coordinate system of the vehicle, P isn't moving at all. :)

 

[Krus]

Hi :)

OK, I'm sorry.. The description was maybe a bit wrong.
I try to explain what I need in some examples:

If v_F = 50 mm/s and α = 0, then the y-component of the velocity would also be 50 mm/s, x-component and ω is then 0.

If v_F = 50 mm/s and α = 90, then the vehicle is turning around its point C -> x-component and ω can't be 0 in point P.

If v_F = 50 mm/s and α = 45, then the vehicle drives in a circle around a center point, which is outside of the vehicle. Then there is a smaller ω than when α = 90, but I have a higher y-component velocity.

I mean in point C, can only exist a y-velocity and an angular velocity. It can't happen that there is a velocity in x-direction. But in point P it is different, because it's not the turning centre.

So there must be a formula, how to calculate the speed in components (x-,y- and angular) for point P.

Sorry, It's kind of difficult to describe the problem :(

 

[haruspex]

I suggest figuring out from the geometry where the centre of rotation is. P then describes an arc about that point.

the component velocity of a point between the front wheel and the center between rear wheels (P) in its local coordinate system.

I guess you mean the co-ordinate system fixed on the ground at the point where P happens to be at this instant, with the y-axis along CP.

 

[Krus]

I guess you mean the co-ordinate system fixed on the ground at the point where P happens to be at this instant, with the y-axis along CP

Yes, you're right, that's what I mean.:)

Do you have any Idea how to get these velocities?
For sure I can get the center of rotation out of the geometry, but how to use these data to get the velocities?

Thanks

 

[haruspex]

For sure I can get the center of rotation out of the geometry, but how to use these data to get the velocities?

Can you figure out the angular velocity?
If you draw a radius from P to the centre of rotation, how long is that radius and what is the direction of movement of P in relation to that?

 

[Krus]

Yes...

The angular velocity and all other values (see image) are the following:

ω = (V_F * sin(α)) / d
r = d / tan(α)

length of radius:
q = √(r² + CP²)

direction of movement of P:
β = atan(CP / r)

 

[haruspex]

Yes...

The angular velocity and all other values (see image) are the following:

ω = (V_F * sin(α)) / d
r = d / tan(α)

length of radius:
q = √(r² + CP²)

direction of movement of P:
β = atan(CP / r)

Yes to all those. I was rather hoping you'd see how to finish it from there.
What is the speed in the direction of movement? What are the x and y components of that?

 

[Krus]

Well, i guess the following:

Speed of movement in P:
v_P = q * ω

Components:
v_PX = V_P * sin(β)
v_PY = V_P * cos(β)

Right? ;)

 

[haruspex]

Well, i guess the following:

Speed of movement in P:
v_P = q * ω

Components:
v_PX = V_P * sin(β)
v_PY = V_P * cos(β)

Right? ;)

Yes, that all looks right.