joeth04
- 17
- 0
Alright I had a midterm in my physics class today, and was completley stumped on this problem. Either I'm missing an equation or just not getting it, if you could lead me in the right direction i'd appreciate it. I also am attaching a picture of the problem that I drew in paint.
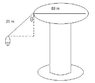
The problem states that the circular ride platform has a diameter of 8.0 meters and the 2.5 m "massless chain" is attached to the chair at an angle theta to vertical. The chair is 10 kg, what is the velocity? I know I forgot to put the decimal points in the attached drawing, it should not make much of a difference either way.
Fc = m*v2/R
v = omega*R
I do not have enough givens for either of these equations.
Homework Statement
The problem states that the circular ride platform has a diameter of 8.0 meters and the 2.5 m "massless chain" is attached to the chair at an angle theta to vertical. The chair is 10 kg, what is the velocity? I know I forgot to put the decimal points in the attached drawing, it should not make much of a difference either way.
Homework Equations
Fc = m*v2/R
v = omega*R
The Attempt at a Solution
I do not have enough givens for either of these equations.