darovmart
- 2
- 0
Hello all, this is my first post here, so please excuse me if there are any mistakes or important information is left omitted. Now, my problem is quite intricate and specific so I will be thankful for any information I can get. Using Excel, I am looking to model the volume flow of air through two interconnected, parallel tubes with different cross-sectional areas A1 and A2. The flow, represented by arrows, comes from a fan as illustrated in the attached image and is distributed through several openings in the lower tube.
My question is, since air flow follows the path of least resistance, what is the precise flow (preferably in the shape of a formula) through each tube at the point where they are first split up?
Pressure loss from air friction is taken into account using the formula ΔP = 0.5 * (L/D) * ρ * λ * v^2, where:
L = Length of the tube in meters
D = Hydraulic diameter of the tube in meters
ρ = density of air, about 1.2 kg/m^3
λ is the Darcy-Weisbach friction coefficient which is determined using the equation shown in the image, where ε represents the tube's roughness in meters and Re the Reynold's number
The leakage flow through the openings in the lower tube is calculated with the following formula:
ΦLeakage = 0.827 * ALeak * P^1.6
Where:
P = the pressure at the point of the leak in Pascals
ALeak = the surface area of the leak in m^2
Secondly, my partner suggested a fictional value for Φ to calculate the pressure loss due to friction, namely ΦΔP which is equal to Φ - (ΦLeakage/2). I am wondering however, if his suggestion is correct. I would also like to know how the the total pressure loss due to friction in both tubes should be taken into account. Again, my partner suggested taking the average of the results and subtracting the outcome from the total local pressure. Any thoughts?
Again, I would like to thank in advance anyone that will try to help me tackle this problem. Good luck.
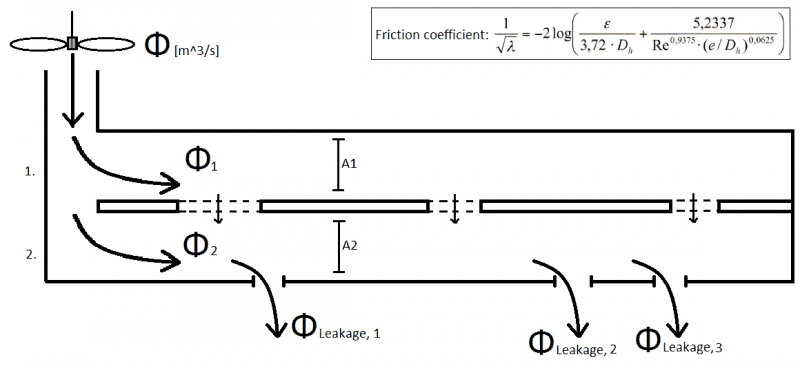
My question is, since air flow follows the path of least resistance, what is the precise flow (preferably in the shape of a formula) through each tube at the point where they are first split up?
Pressure loss from air friction is taken into account using the formula ΔP = 0.5 * (L/D) * ρ * λ * v^2, where:
L = Length of the tube in meters
D = Hydraulic diameter of the tube in meters
ρ = density of air, about 1.2 kg/m^3
λ is the Darcy-Weisbach friction coefficient which is determined using the equation shown in the image, where ε represents the tube's roughness in meters and Re the Reynold's number
The leakage flow through the openings in the lower tube is calculated with the following formula:
ΦLeakage = 0.827 * ALeak * P^1.6
Where:
P = the pressure at the point of the leak in Pascals
ALeak = the surface area of the leak in m^2
Secondly, my partner suggested a fictional value for Φ to calculate the pressure loss due to friction, namely ΦΔP which is equal to Φ - (ΦLeakage/2). I am wondering however, if his suggestion is correct. I would also like to know how the the total pressure loss due to friction in both tubes should be taken into account. Again, my partner suggested taking the average of the results and subtracting the outcome from the total local pressure. Any thoughts?
Again, I would like to thank in advance anyone that will try to help me tackle this problem. Good luck.