toiletmirror
- 2
- 0
Hi all,
I'd like to confirm my understanding on some things regarding pressure losses in a branched pipe for a project.
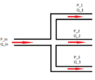
Referring to the picture below I grabbed off from the net. (assume no elevation chan
Would appreciate if someone can correct me if I'm wrong anywhere.
1) Total pressure (Pt) = Static pressure (Ps) + Dynamic pressure (Pd)
2) A pressure gauge connected to the side of the pipe (with flowing fluid) only measures static pressure
3) Q(in) = Q(1) + Q(2) + Q(3) [by continuity]
Assuming no minor losses,
4) V(in) = 3*V(1) = 3*V(2) = 3*V(3) [for A(1) = A(2) = A(3) = A(in)]
5) Pt(in) = Pt(1) = Pt(2) = Pt(3)
6) So for Pd = rho*V²/2: Pd(in) = 9*Pd(1) = 9*Pd(2) = 9*Pd(3)
7) Hence by Bernoulli's, to balance the pressures (energies) : 9*Ps(in) = Ps(1) = Ps(2) = Ps(3)
8) My pressure gauges at each of the branch will read at a pressure 9 times higher than that at the main branch
Assuming minor losses due to the branching and bends
9) Solving the same way as previously, but now I need to substract pressure due to minor loss from Pd at each branches
10) Use Darcy-Weisbach, find friction factor and use equivalent length
11) I can individually look at a branch to do this [i.e. Inlet to outlet1 or inlet to outlet2 etc.]
12) Substract pressure loss in (11) to each of the 3 branch to account for the total pressure difference
13) However my gauge will still read static pressures only, so will not pick up these minor losses (Hence reading at branch 1 will still be equal to that at branch 2)Am I correct in the 13 steps I posted? Thank you!
I'd like to confirm my understanding on some things regarding pressure losses in a branched pipe for a project.
Referring to the picture below I grabbed off from the net. (assume no elevation chan
Would appreciate if someone can correct me if I'm wrong anywhere.
1) Total pressure (Pt) = Static pressure (Ps) + Dynamic pressure (Pd)
2) A pressure gauge connected to the side of the pipe (with flowing fluid) only measures static pressure
3) Q(in) = Q(1) + Q(2) + Q(3) [by continuity]
Assuming no minor losses,
4) V(in) = 3*V(1) = 3*V(2) = 3*V(3) [for A(1) = A(2) = A(3) = A(in)]
5) Pt(in) = Pt(1) = Pt(2) = Pt(3)
6) So for Pd = rho*V²/2: Pd(in) = 9*Pd(1) = 9*Pd(2) = 9*Pd(3)
7) Hence by Bernoulli's, to balance the pressures (energies) : 9*Ps(in) = Ps(1) = Ps(2) = Ps(3)
8) My pressure gauges at each of the branch will read at a pressure 9 times higher than that at the main branch
Assuming minor losses due to the branching and bends
9) Solving the same way as previously, but now I need to substract pressure due to minor loss from Pd at each branches
10) Use Darcy-Weisbach, find friction factor and use equivalent length
11) I can individually look at a branch to do this [i.e. Inlet to outlet1 or inlet to outlet2 etc.]
12) Substract pressure loss in (11) to each of the 3 branch to account for the total pressure difference
13) However my gauge will still read static pressures only, so will not pick up these minor losses (Hence reading at branch 1 will still be equal to that at branch 2)Am I correct in the 13 steps I posted? Thank you!