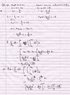Fluid mechanics - submerged triangular surfaces

[TimIgoe90]

Hi, i am having difficulty with a question because i cannot seem to get the right answer. i don't think i am far off i just know i go wrong somwhere and if you could point that out it would be great. the question is attatched. for the first part i find the equations of the lines of the two sides starting from d. then subtract them to find w (=Xright-Xleft). using double integration i find the area by
A=∫∫dA where limits firstly are X=Xright, X=Xleft and then S=h and S=0. My problem is on part C i cannot get the correct answer which means i have gone somewhere wrong further up, most likely at either the limits I am using or for S or finding w. I am meant to use double integration for these questions and Sc=As|o /A and ***|c= ***|o - A*Sc^2.
Any comments are appreciated, thanks

 

[tiny-tim]

Welcome to PF!

Hi TimIgoe90! Welcome to PF!

… for the first part i find the equations of the lines of the two sides starting from d. then subtract them to find w (=Xright-Xleft).

fine so far

using double integration i find the area by A=∫∫dA where limits firstly are X=Xright, X=Xleft and then S=h and S=0. My problem is on part C i cannot get the correct answer which means i have gone somewhere wrong further up, most likely at either the limits …

yup, your limits can't both be between fixed numbers

if your S limits are from 0 to h, then your x limits will be functions of S

(= the left- and right-most coordinates of that strip in the diagram, of height dh )

 

[TimIgoe90]

I am sorry not sure i understand. i have found w to be = Xright-Xleft by finding the equation of the lines in terms of S and functions of S. so w= [(b-d)*s/ λh]+[d*s/h]. from my notes i am told that my limits for x should be xleft and xright, which when integrating A=∫∫dA it would give me A=∫wds...what two limits of s would i then need to integrate it? sorry if you already answered but i wasnt sure. thanks

 

[tiny-tim]

i have found w to be = Xright-Xleft by finding the equation of the lines in terms of S and functions of S. so w= [(b-d)*s/ λh]+[d*s/h]. from my notes i am told that my limits for x should be xleft and xright, which when integrating A=∫∫dA it would give me A=∫wds...what two limits of s would i then need to integrate it?

the limits of S are 0 to h

 

[TimIgoe90]

the limits of S are 0 to h

thats what i thought it was. but i cannot seem to get the correct answer for part C. I am not sure where i am going wrong, my answer is close to the required one, so i don't think i am too far off.

 

[tiny-tim]

if you want us to check your work, you'll have to show us

 

[TimIgoe90]

That is my working out. Much appreciated

 

[tiny-tim]

it's a little difficult to read, but i think your answer for A is wrong,

you seem to have lost a 1/λ somewhere