Fluid Mechanics: Tilted Axes and Weight of Gate

[wahaj]

Homework Statement

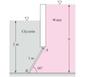
AB is homogeneous with mass of 180 kg, goes 1.2m in the page and is hinged at A and resting on aa smooth bottom at B. All fluids at 20 C. Find height of water that will result on 0 force at B

Homework Equations

M_s = \int\int_s \ (\vec{r} \times \hat{n} )PdA
\frac{dP}{dy} = \rho \vec{g}

The Attempt at a Solution

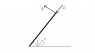
The approach I am using to solve this problem is that the total moment caused at point is equal to 0. Therefore the moment caused by glycerine must be equal to the moment caused by water. The problem with this approach is that it neglects the weight of the mass. The bigger problem I have is that I can't seem to work with the axes. I know that the origin has to be at A. If I choose to set the positive z axis downwards along AB and the positive x-axis perpendicular to AB towards the left, the positive y-axis will go into the page. With axes defined the parts of the equation for pressure are \vec{r} = z\hat{k} and \hat{n} = \hat{i} I found \vec{g} = \ -gcos(60) \vec{i} + gsin(60)\vec{k} I am having trouble working out the geometry of the height of the fluid. Can someone check what I already have and help me with the height vector and dA?

 

[SteamKing]

I think your choice of axes is going to make solving this problem more complicated than it needs to be.

 

[wahaj]

Already tried is using regular axes. They made it even harder. Also my prof said to use tilted axes for tilted gates

 

[Chestermiller]

You're on the right track. How is dz along the gate related to a differential change in depth dD?How is a differential change in pressure dp related to a differential change in depth, dD? How is a differential change in pressure related to a differential distance dz along the gate?

Chet

 

[wahaj]

dD = dz \ sin(60) \\ <br /> P = \rho gdD \\<br /> dP = \rho g sin(60) dz
I think I did this right. Anyways I actually figured the question out and got the right answer around the time I made my last post. Thanks for the help though