dRic2
Gold Member
- 887
- 225
Hi PF,
I'm trying to derive the Prandlt condition (not sure if it is Prandlt's work tough) for a fluid to separate from a surface in the boundary layer. The equation should be:
##\frac {\partial^2 v_x} {\partial y^2} = 0##
which is quite "intuitive" to me.
To derive it let's start from the simplified version of NS equations: the boundary layer equation derived under Prandlt's assumpions
##v_x \frac {\partial v_x} {\partial x} + v_y \frac {\partial v_x} {\partial y} = \nu \frac {\partial^2 v_x} {\partial y^2} + \frac 1 {\rho} \frac {dp} {dx}##
and the continuity equation
##\frac {\partial v_x} {\partial x} + \frac {\partial v_y} {\partial y} = 0##
Now, I found on my professor's notes that (hope my translation will be good enough):
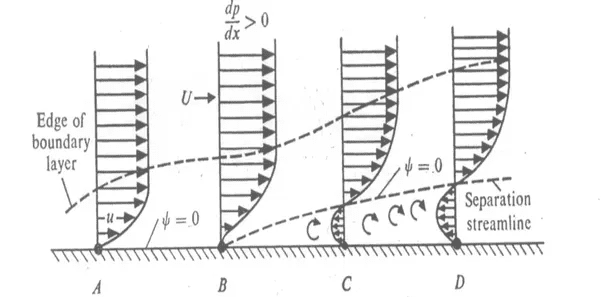
I can't understand why ##\frac {\partial v_x} {\partial y} |_{y=0} = 0##. Does someone have a clue?If a sketch is need I found this picture online:
I'm trying to derive the Prandlt condition (not sure if it is Prandlt's work tough) for a fluid to separate from a surface in the boundary layer. The equation should be:
##\frac {\partial^2 v_x} {\partial y^2} = 0##
which is quite "intuitive" to me.
To derive it let's start from the simplified version of NS equations: the boundary layer equation derived under Prandlt's assumpions
##v_x \frac {\partial v_x} {\partial x} + v_y \frac {\partial v_x} {\partial y} = \nu \frac {\partial^2 v_x} {\partial y^2} + \frac 1 {\rho} \frac {dp} {dx}##
and the continuity equation
##\frac {\partial v_x} {\partial x} + \frac {\partial v_y} {\partial y} = 0##
Now, I found on my professor's notes that (hope my translation will be good enough):
The point of separation indicates the transition (near the surface) between different currents flowing in opposite directions, thus ##\frac {\partial v_x} {\partial y} |_{y=0} = 0##
I can't understand why ##\frac {\partial v_x} {\partial y} |_{y=0} = 0##. Does someone have a clue?If a sketch is need I found this picture online: