Fluid velocity in free jets doubt

Click For Summary

Discussion Overview

The discussion revolves around the fluid velocity in free jets, particularly focusing on the application of Bernoulli's equation in scenarios involving nozzles and varying cross-sectional areas. Participants explore the implications of fluid dynamics principles in both ideal and real-world contexts, addressing concepts such as acceleration, pressure changes, and the assumptions underlying the equations used.

Discussion Character

  • Exploratory
  • Technical explanation
  • Debate/contested
  • Mathematical reasoning

Main Points Raised

  • Some participants express confusion about how a nozzle accelerates fluid, questioning the source of the motive force.
  • Others argue that the nozzle accelerates the flow due to the continuity equation and a reduction in static pressure.
  • It is noted that Bernoulli's equation may not apply inside the nozzle due to the presence of shear and vorticity.
  • Some participants assert that buoyancy is the force acting on an open container, while others contend that hydrostatic pressure is the relevant force.
  • There is a discussion about the application of Bernoulli's equation at various points in the system, with some suggesting that pressure at points before and after the nozzle may not be equal due to energy conversion.
  • One participant proposes a method for solving the problem by identifying key points and applying Bernoulli's equation, while others challenge the assumptions made regarding pressure and velocity.
  • Concerns are raised about the assumptions of ideal fluid behavior, with some participants emphasizing the complexities introduced by viscosity and boundary layers in real fluids.

Areas of Agreement / Disagreement

Participants do not reach a consensus on the application of Bernoulli's equation in this context, with multiple competing views regarding the behavior of fluid in nozzles and the forces involved. The discussion remains unresolved with respect to the correct interpretation of fluid dynamics principles.

Contextual Notes

Limitations include assumptions about ideal fluid behavior, the impact of viscosity, and the applicability of Bernoulli's equation in real-world scenarios. Participants acknowledge that the presence of vorticity and shear complicates the analysis.

R Power
Messages
270
Reaction score
0
Hi friends
This isn't a homework poblem. However,I got this confusion when i was solving some problems.
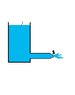
Consider fluid flowing out of a tank as shown in figure attached.
Fluid moves out of pipe through a nozzle (generally used to accelerate the fluid). Now if we apply bernoulli's equation at point 1 and 2(shown in fig.) we find that fluid velocity comes out to be: V= (2gh)^1/2 (where h is height of tank above nozzle)
which is independent of nozzle diametre. That means if i remove the nozzle and fluid flows through a pipe of constant cross section, then also velocity will be same. This can be checked by applying bernoulli's equation.
But in general nozzle accelerates the fluid for same mass flow rate.
How will you explain this?
 

Attachments

  • Untitled.jpg
    Untitled.jpg
    4.3 KB · Views: 430
Physics news on Phys.org
R Power said:
Fluid moves out of pipe through a nozzle (generally used to accelerate the fluid).

You lost me here. How does a nozzle accelerate the fluid? Where is the motive force?
 
This is just an estimate for the velocity. Strickly speaking it is applied only before the nozzle. Because inside the nozzle the flow has mean shear (vorticity is not zero), thus the flow is no longer potential and the bernoulli's equation does not apply.

P.S. do not read crappy wiki articles, read proper books.
 
Andy Resnick said:
You lost me here. How does a nozzle accelerate the fluid? Where is the motive force?

Its accelerating the flow via the continuity equation. The force is coming in the form of reduction in static pressure.
 
zeebek said:
This is just an estimate for the velocity. Strickly speaking it is applied only before the nozzle. Because inside the nozzle the flow has mean shear (vorticity is not zero), thus the flow is no longer potential and the bernoulli's equation does not apply.

P.S. do not read crappy wiki articles, read proper books.

Assume it's isentropic! :-p
 
Cyrus said:
Its accelerating the flow via the continuity equation. The force is coming in the form of reduction in static pressure.

Not so fast... the force is bouyancy, acting on the open container. If the container were sealed, there won't be any flow.

The nozzle does not *accelerate* the flow... re-direct, at best.
 
Andy Resnick said:
Not so fast... the force is bouyancy, acting on the open container. If the container were sealed, there won't be any flow.

The nozzle does not *accelerate* the flow... re-direct, at best.

If you have a nozzle, the flow velocity coming in is less than the flow going out (again, just look at the contiunity equation). So the flow had to accelerate. Also, the force acting on the open container is not bouyancy, it is hydrostatic. :smile:

To be more precise, let's just look at what the math says:

A_i V_i = A_e V_e

where e - exit, and i - inlet. Then clearly:

V_{e} = \frac{A_i}{A_e}V_i

But by definition the ratio of the areas is > 1 for a nozzle. Hence the flow speeds up. By Bernoulli, the static pressure goes down. This causes a static pressure gradient across the nozzle (a bouyancy force), which pushes the nozzle in the axial direction inline to the flow contraction. Take a garden hose and put your thumb over it, you will feel this force as it pushes your hand forward.

We correct for this type of problem in the wind tunnel for large models.
 
Last edited:
This is just an estimate for the velocity. Strickly speaking it is applied only before the nozzle. Because inside the nozzle the flow has mean shear (vorticity is not zero), thus the flow is no longer potential and the Bernoulli's equation does not apply.

P.S. do not read crappy wiki articles, read proper books.
I am reading FM by munson young and okishi which is one of the very good books on the subject as far as i know. And author applies bernoulli's equation as i did.
 
so what's the solution to my problem?
 
  • #10
R Power said:
so what's the solution to my problem?

You applied your analysis incorrectly. Go back and do it over again, and have point two just before the nozzle, and a new point three just after the nozzle. See what you get.
 
  • #11
if i take point 2 just before the nozzle and then i apply bernoulli, i can't find velocity at 2 because i don't know pressure at 2.
Can u help
 
  • #12
R Power said:
if i take point 2 just before the nozzle and then i apply bernoulli, i can't find velocity at 2 because i don't know pressure at 2.
Can u help

I tried working this problem out, here is what I would do. Make three points, 1 (top of the tank), 2 (bottom of the tank), 3 (nozzle entrance), 4 nozzle exit.

I would solve this by finding the pressure at point 2, which is just hydrostatic. That will be the total pressure (with zero velocity). Use that as your inlet condition to the nozzle (3), and find the flow velocity at (4).Side note: I is capitalized, and u is spelled "you". The first letter of a sentence is capitalized, and the sentence ends in a period.
 
  • #13
Are you sure static pressure at points 2 and 3 would be same?
Since fluid moves from 2 to 3 and since elevation remains constant, so all the pressure energy in converted into kinetic energy and that's why velocity increases in pipe and so static pressure decreases there, so pressure at 2 won't be equal to that at 3.
 
  • #14
Strictly speaking, no the pressure won't be the same (your observation is correct). I neglected, and thinking twice about it you probably shouldn't. Try writing out the equations, (with the pressure as an unknown). And then see if you can eliminate it later on. I.e, write the equations from 1-2, 2-3, 3-4. Then see if things will drop out. If you write said equations here, we can try and look at them together.
 
  • #15
1-2 pgh = P2 (p = density of water) (P2 = pressure at 2)

2-3 P2 = P3 + [0.5 * p * (V3)^2] (V3 = velocity at 3)

3-4 P3 + [0.5 * p * (V3)^2] = 0.5 p (V4)^2
 
  • #16
come on cyrus i have wrote the equations , now help me !
 
  • #17
I am going to give you one more reply

if we assume the liquid has no viscosity (ideal fluid) than bernulli is applied before and after the nozzle. In this case there is veolicty slip at the wall, it does not go to zero like in reality. Then the velocity before the nozzle and after the nozzle not going to change. By nozzle here I mean a tube of constant cross section like in your figure. If the cross section does change, then the velocity will increase in case the cross section is shrinking and vice versa like Cyrus wrote.

However, in reality there is no slip at the wall, slowly boundary layer will be develloping, the flow in the middle of the tube will accelerate. Also, since there will be definitely vorticity in the tube, bernulli is not applied. I am not going to go into details here, but there are many reasons why velocity in the outlet not going to be the same as near the inlet besides just varying cross section. Meanwhile, provided the nozzle is of constant diameter and not very long, this estimate from bernullli equation is reasonably correct.

P.S. Never heard about the book you mention. Proper well known books are: Batchelor - Introduction to fluid mechanics, Kundu - Fluid Mechanics, etc.
 
Last edited:

Similar threads

Undergrad Exit velocity through a nozzle: Bernoulli vs. Experience
  • · Replies 7 ·
Replies
7
Views
4K
Graduate How Does Jet Injection Work in Fluid Dynamics?
  • · Replies 6 ·
Replies
6
Views
2K
Undergrad Bernoulli and Momentum Disconnect?
  • · Replies 4 ·
Replies
4
Views
2K
Undergrad Work - Energy Principle Application to Fluid Flow
  • · Replies 35 ·
2
Replies
35
Views
5K
Undergrad Bernoull's Equation Derivation From Work - Energy Principle
  • · Replies 20 ·
Replies
20
Views
3K
Undergrad Understanding Bernoulli's Principle
  • · Replies 43 ·
2
Replies
43
Views
7K
Undergrad Work - Energy Principle Application to Fluid Flow
  • · Replies 48 ·
2
Replies
48
Views
5K
High School Torricelli's Theorem: Speed of Fluid & Height of Opening
  • · Replies 4 ·
Replies
4
Views
2K
Undergrad Assumptions for Navier Stokes equations in this system
  • · Replies 3 ·
Replies
3
Views
1K
Graduate Why are the Navier-Stokes equations inconsistent in this case?
  • · Replies 18 ·
Replies
18
Views
3K