Flux induced in a circular loop

[meaghan]

Homework Statement

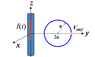
I have a circular loop with a radius of 1 m. The center of the loop is located 2 m away from a infinitely long current carrying wire, with ac current I. Find the flux in the circular loop

Homework Equations

Φ = ∫ B ds

The Attempt at a Solution

I've found a lot of examples with square loops, so the magnetic field in the loop will depend on both the x and y direction.
I got that Φ = ∫ u_o I / π(2+y) *√(1-y²) since the magnetic field will change according to the point on the circle.

 

[Chandra Prayaga]

A diagram is always helpful. From your statement, it is not clear if the circular loop and the long wire are in one plane.

 

[meaghan]

it's all in one plane

 

[Chandra Prayaga]

How did you write the integral for the flux?

 

[meaghan]

How did you write the integral for the flux?

Φ = ∫ u_o I √(a²+y²) / (π (2a+y)) dy

 

[Chandra Prayaga]

My question was, do you know how that integral was derived?