Condensate
- 20
- 0
[Solved] Force Accelerating Two Identical Touching Blocks
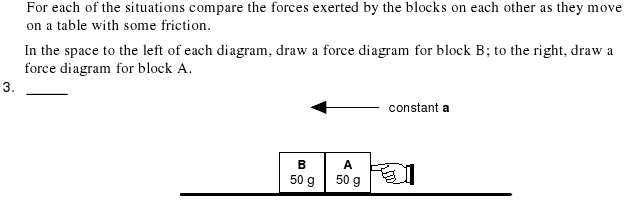
The two blocks are accelerating at a constant rate due to the force of the hand, and air resistance is ignored.
I'll go beyond the question above and try to find why FB and FA are less than Fhand mathematically, since that would greatly help my conceptual understanding.
My mathematical assumptions (not given in the question, just there so that I can try and figure out the above mathematically):
μ = 0.2
Acceleration= 3
Fhand= 200 N
m=0.05 kg
Normal Force= 0.5 N
Force(A)net = Fhand + Ffriction + FB
Force(B)net = FA + Ffriction
Ffriction= μFN
F = ma
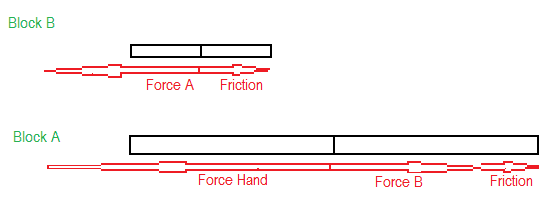
3a. Conceptual chart attempt at a solution (Boxes are just to show the scaling and boxes for A are not equivalent to those for B)
3b. Mathematical attempt at a solution
Finding Ffriction for Block A using Ffriction= μF:: Can be repeated for Block B
4. What it comes down to:
[STRIKE]-Was I wrong in assuming that F= ma = Forcenet of an object?
-How come the force of A exerted by Block A on Object B is less than Force of the Hand on Object A (and is this even true?) Is there a mathematical way to figure this out? My attempt gave different frictions for both blocks.
-Do any of the assumptions appear to mess up the math?
-Do the force diagrams accurately portray acceleration and the horizontal forces on both of the blocks?[/STRIKE]
So, any amount of help from you guys would be super appreciated!
Edit: When finding the actual acceleration from a single 100 g block and using that in the 50 g block equations, everything fit perfectly.
Homework Statement
The two blocks are accelerating at a constant rate due to the force of the hand, and air resistance is ignored.
I'll go beyond the question above and try to find why FB and FA are less than Fhand mathematically, since that would greatly help my conceptual understanding.
My mathematical assumptions (not given in the question, just there so that I can try and figure out the above mathematically):
μ = 0.2
Acceleration= 3
Fhand= 200 N
m=0.05 kg
Normal Force= 0.5 N
Homework Equations
(only for X forces):Force(A)net = Fhand + Ffriction + FB
Force(B)net = FA + Ffriction
Ffriction= μFN
F = ma
3a. Conceptual chart attempt at a solution (Boxes are just to show the scaling and boxes for A are not equivalent to those for B)
3b. Mathematical attempt at a solution
Finding Ffriction for Block A using Ffriction= μF:: Can be repeated for Block B
- Ffriction for Block A= μFN
- Ffriction for Block A= 0.2 x 0.5 (Subsitituting in the values)
- Ffriction for Block A= 0.1
- F = ma = Forcenet
- Force(A)net = Fhand + Ffriction + FB
- Force(A)net = Fhand + Ffriction + FB= ma (Substituting net force of Block A for f)
- Force(A)net = 200 + (-0.1) + FB= 0.15 (Substituting in the values)
- 199.9 + FB= 0.15
- FB= -199.75 => FA=199.75
- Force(B)net = FA + Ffriction= ma
- 199.75 + Ffriction= 0.15 (Substituting in the values)
- Ffriction= -199.6
- Ffriction= μFN
- Ffriction= 0.2 x 1 (Substituting in the values)
- Ffriction= 0.2
- Forcenet = Fhand + Ffriction= ma
- 200 + Ffriction = 0.3 (Substituting in the values)
- Ffriction = -199.7
4. What it comes down to:
[STRIKE]-Was I wrong in assuming that F= ma = Forcenet of an object?
-How come the force of A exerted by Block A on Object B is less than Force of the Hand on Object A (and is this even true?) Is there a mathematical way to figure this out? My attempt gave different frictions for both blocks.
-Do any of the assumptions appear to mess up the math?
-Do the force diagrams accurately portray acceleration and the horizontal forces on both of the blocks?[/STRIKE]
So, any amount of help from you guys would be super appreciated!
Edit: When finding the actual acceleration from a single 100 g block and using that in the 50 g block equations, everything fit perfectly.
Last edited: