Force and Torque exerted on a dipole system from a point charge

[binbagsss]

I have attached a diagram.
s
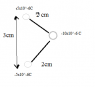
Three charge are at corners of an triangle. The + and - 5.00*10^-6C charges form a dipole.
a) Find the magnitude and direction of the force exerted on the dipole from the -10*10^-6C charge.
b) For an axis perepndiculat to the line connected the + and - 5.00*10^-6C charges , find the torque exerted on the dipole by the -10*10^-6 C charge, direction and magnitude?


My attempt:
a) The net force = 0.
Its magnitude on both charges = 1125 N, (from Coloumb's law and using r as 2cm.

However the answer is 1680N on both charges respectively.

b) Torque = Force * distance perpendicular to the line of action.

Considering a single charge, the force exerted on it is 1125N, and the distance perpendicular to the line of action 1.5cm.

The net torque will then = 2(1.5*10^-2 * 1125) , as the force acts in opposite directions on both charges, consequently rotating the dipole system in the same way.

T = 33.75N.m

(The correct answer is however 22.3N.m)F

 

[ehild]

The question is the force exerted on the whole dipole. You have to add the forces exerted on the separate charges, taking their directions into account.

ehild