Hijaz Aslam
- 66
- 1
Consider the pith balls in the diagram:
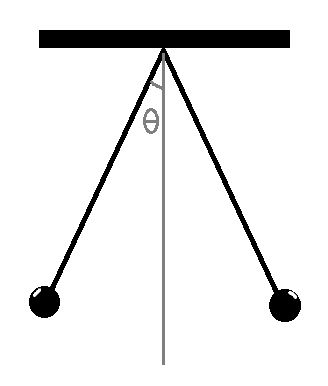
Both of them has mass 'm' and charge 'q'. The question asks for the charge on both the pith balls.
The concept is a bit straightforward. But I am confused at the force distribution experienced by the pith balls.
My text tackles the problem with reference to the following diagram.

And taking ##Tcos\theta=g## and then using ##T=\frac{g}{cos\theta}## and then proceeding to find the charge.
The part I am confused with is that, if we consider the following image

why can't we resolve the vectors as shown in the image and use ##T=gcos\theta## and proceed?
Is it because the tension has a component perpendicular to that of 'g' ?
I am confused with the Free Body Diagram of forces. Is there any good article available on web?
Both of them has mass 'm' and charge 'q'. The question asks for the charge on both the pith balls.
The concept is a bit straightforward. But I am confused at the force distribution experienced by the pith balls.
My text tackles the problem with reference to the following diagram.
And taking ##Tcos\theta=g## and then using ##T=\frac{g}{cos\theta}## and then proceeding to find the charge.
The part I am confused with is that, if we consider the following image
why can't we resolve the vectors as shown in the image and use ##T=gcos\theta## and proceed?
Is it because the tension has a component perpendicular to that of 'g' ?
I am confused with the Free Body Diagram of forces. Is there any good article available on web?