dykuma
- 55
- 6
- Homework Statement
- I am given the electric and magnetic field, ## \vec E= \alpha x \hat x## and ## \vec B= \beta x \hat y##, where ##\alpha## and ##\beta## are constants. It is assumed that neither field is changing in time.
I am then asked to find the electromagnetic 'force per volume' (which I believe to be the 'force density'), as well as the 'power per volume' that's converted from electromagnetic energy into mechanical energy. Lastly, I'm asked to find a form of ##\alpha## and ##\beta## that makes the force density equal zero, besides both of them equaling zero.
- Relevant Equations
- $$\vec F_V = \rho \vec E + \vec J \times \vec B$$
possibly (not sure if this is correct) that work per volume is
$$ W_V = \frac {\varepsilon_0 \vec E^2} { \ 2 } + \frac {\vec B^2} { \ \mu_0 2 } $$
My guess is that the force per volume is:
$$ \vec F_V = \rho \alpha x \hat x + \vec J \times \beta x \hat y$$
but I'm not sure where to go after that. I'm not given a value for either the charge density or the current density, so I can't simplify the relation much. Further, I'm not sure if my equation for the "work per volume" is correct. however, it's my best guess for what's being asked for.
Edit:
I've made some progress, which I've attached below. The issue is that I'm suppose to find conditions for that make the force vanish, without having the terms themselves be zero. I can't do this, because the only way for the force volume to be zero is for 'x' to be zero, or for alpha to be zero. (my understanding is that ##\alpha## and ##\beta## need to be related to each other so that the constant's themselves sum the force volume relation to zero).
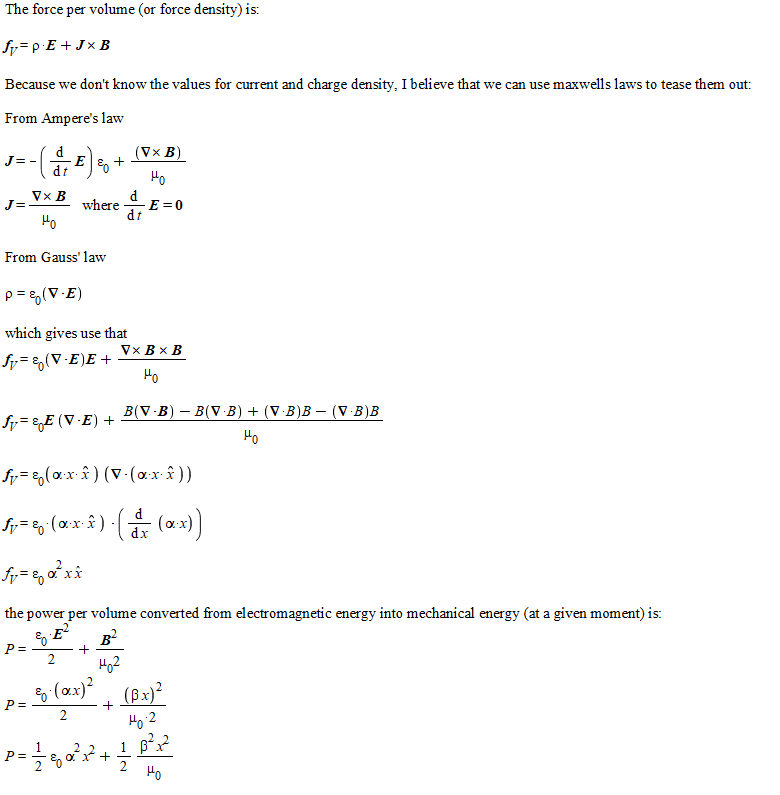
$$ \vec F_V = \rho \alpha x \hat x + \vec J \times \beta x \hat y$$
but I'm not sure where to go after that. I'm not given a value for either the charge density or the current density, so I can't simplify the relation much. Further, I'm not sure if my equation for the "work per volume" is correct. however, it's my best guess for what's being asked for.
Edit:
I've made some progress, which I've attached below. The issue is that I'm suppose to find conditions for that make the force vanish, without having the terms themselves be zero. I can't do this, because the only way for the force volume to be zero is for 'x' to be zero, or for alpha to be zero. (my understanding is that ##\alpha## and ##\beta## need to be related to each other so that the constant's themselves sum the force volume relation to zero).
Last edited: