Force Diagrams for Sliding Block on Inclined Plane

[opus]

Homework Statement

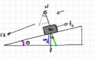
This is more of a general question, not specific to any problem. I am not too good at drawing force diagrams so I was hoping I could post an image and get some guidance on how to find the forces acting on the object.
In this case, we have a block sliding down a plane of angle θ and a coefficient of kinetic friction μ.
My troubles usually lie with breaking the normal force and gravitation force down to components that are acting along the plane. Here I have made the plane the x axis, with down the plane being positive.

To me it seems as the component of the normal force acting along the plan should be $mgcos(\theta)$. $f_k$ will I believe be μN (not any particular component of N, but just N). I am unsure of the gravitational component though.

Please see my attached image. Thank you.

Homework Equations

The Attempt at a Solution

 

[PeroK]

A couple of things. First, when you have an incline you need to break each force down into a components normal to and parallel to the incline. The first force you need to do this for is gravity.

The "normal" force is already normal to the plane. So, that doesn't need to be further broken down. $N_x = 0$ by definition. There is no normal force parallel to the incline.

Moreover, the normal force must balance the gravitational normal force: this is because the incline is solid and prevents motion normal to its surface.

Finally, you have friction as a resisting force. As friction acts to resist motion and motion is constrained to be parallel to the incline, then the frictional force must be in that direction. So, again, the friction force doesn't need to be broken down further.

 

[opus]

Ok, so then if we have the component of gravity that is normal to the plane, it will be equal in magnitude and opposite in sign to the normal force. So first thing to do is to get the normal component of gravity as you said. I don't think I quite understand the best method to do this when I have an incline. If you have a look at my attached image, it can be shown that the angles in pink are equal and this should help me get the normal component of gravity (labeled in green).
So wouldn't the green portion be the hypotenuse of a right triangle and can be represented as $\frac{mg}{cos(\theta)}$?

 

[PeroK]

Ok, so then if we have the component of gravity that is normal to the plane, it will be equal in magnitude and opposite in sign to the normal force. So first thing to do is to get the normal component of gravity as you said. I don't think I quite understand the best method to do this when I have an incline. If you have a look at my attached image, it can be shown that the angles in pink are equal and this should help me get the normal component of gravity (labeled in green).
So wouldn't the green portion be the hypotenuse of a right triangle and can be represented as $\frac{mg}{cos(\theta)}$?

The force itself, $mg$, is the length of the hypotentuse. The components must each be shorter. Try this:

https://www.khanacademy.org/science...d-planes-ap/v/inclined-plane-force-components

Note that in general, for any vector, if you choose your axes so that the vector is inclinded at an angle $\theta$ to your axes, then its components are $(v \cos \theta, v \sin \theta)$

You always need to be careful which one is in which direction as it's easy to get sines and cosines mixed up.

 

[opus]

Ok that video was very helpful. My component triangle for gravity was messed up and had the wrong leg as the hypotenuse. So now we have the gravitational force perpendicular to the plane is $mgcos(\theta)$ and the component parallel to the plane is $mgsin(\theta)$. Since the block isn't moving in a perpendicular fashion to the plane, $mgcos(\theta)$ must be canceled by the normal force. So I guess we could say that $F_N = -mgcos(\theta)$.
So then, since the normal only acts perpendicularly to the the plane, is the only thing that is moving the block down the plane the force component of gravity that is parallel to the plane ie $mgsin(\theta)$?

 

[opus]

Picture for reference

 

[PeroK]

Ok that video was very helpful. My component triangle for gravity was messed up and had the wrong leg as the hypotenuse. So now we have the gravitational force perpendicular to the plane is $mgcos(\theta)$ and the component parallel to the plane is $mgsin(\theta)$. Since the block isn't moving in a perpendicular fashion to the plane, $mgcos(\theta)$ must be canceled by the normal force. So I guess we could say that $F_N = -mgcos(\theta)$.
So then, since the normal only acts perpendicularly to the the plane, is the only thing that is moving the block down the plane the force component of gravity that is parallel to the plane ie $mgsin(\theta)$?

Yes, that's it.

 

[opus]

Ok great, so to summarize let me see if I can get the final result correct.
We have $mgsin(\theta)$ pushing the block down the plane. If we have friction to consider, it will be acting opposite of the motion. Friction is represented as μN. Since N is equal in magnitude and opposite in direction of the normal component of gravity, we can say that $N=-mgcos(\theta)$. So the if the block is moving we have $F_f=μN=-μmgcos(\theta)$
So to represent all forces acting on the block, can I say that $F_{net}=mgsin(\theta)-μmgcos(\theta)$?

 

[PeroK]

Ok great, so to summarize let me see if I can get the final result correct.
We have $mgsin(\theta)$ pushing the block down the plane. If we have friction to consider, it will be acting opposite of the motion. Friction is represented as μN. Since N is equal in magnitude and opposite in direction of the normal component of gravity, we can say that $N=-mgcos(\theta)$. So the if the block is moving we have $F_f=μN=-μmgcos(\theta)$
So to represent all forces acting on the block, can I say that $F_{net}=mgsin(\theta)-μmgcos(\theta)$?

Yes, exactly. One thing to remember is that is The maximum friction force and that equation applies if the block is moving.

 

[opus]

So if the block is stationary, I cannot use μN=-mgcos(θ)?

 

[PeroK]

So if the block is stationary, I cannot use μN=-mgcos(θ)?

No. If the block is stationary tgen the frictional force equals the opposite of the gravitational force down the incline.

 

[opus]

Thanks!

 

[haruspex]

One thing to remember is that is The maximum friction force and that equation applies if the block is moving.

To clarify, the formulae for static and kinetic friction are slightly different:
$|F_k|=\mu_k|N|$
$|F_s|\leq \mu_s|N|$