- #1
dookedoo
- 2
- 0
Help - Force on a Current in a Magnetic Field
Magnetic and gravitational forces
A horizontal wire is hung from the ceiling of a room by two massless strings. A uniform magnetic field is directed from the ceiling to the floor. When a current exists in the wire, the wire swings upward and makes an angle with respect to the vertical (wire is in equilibrium).
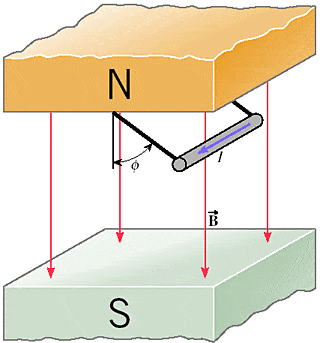
The wire has a length of 0.20 m and a mass of 0.065 kg and carries a current of 42 A. The magnitude of the magnetic field is 0.060 T.
(e) What is the algebraic expression for the angle in the drawing? Express your answer in terms of the current I in the wire, the length L of the wire, the magnitude B of the magnetic field, the mass m of the wire, and the magnitude g of the acceleration due to gravity.
F = ILB sin(theta)
While this is a relatively easy problem, I still can't see what mistake I am making.
First, given that the wire is in equilibrium,
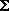 Fx = 0 and
Fx = 0 and
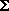 Fy = 0
Fy = 0
The three forces acting on the wire in the question are Tension in the two
Strings, the magnetic force from the magnetic field acting on the wire, and the force of gravity.
Using right hand rule, the magnetic force points to the right. It has to be perpendicular to the magnetic field and current (current replacing the velocity component in the right hand rule)
Knowing this, three equations are generated:
2T = Tension of two strings
the tension can be resolved into x and y components
x-component = 2Tsin(theta)
y-component = 2Tcos(theta)
Magnetic Force = ILBsin(theta) going to the right
Force of Gravity = mg going down
using Netwon's second law,
2Tcos(theta) - mg = 0
2T = mg / (cos(theta)) // solving for 2T using y-components
2Tsin(theta) - ILBsin(theta) = 0
2Tsin(theta) = ILBsin(theta) // solving for theta
2T = ILB
mg / (cos(theta)) = ILB // substitution from previous equation
mg / ILB = cos(theta)
arccos( mg / ILB ) = theta
This is the answer I arrived at for question (e), but according to my online problem set this answer is incorrect. If any insight could be given that would be great. Thanks!
Homework Statement
Magnetic and gravitational forces
A horizontal wire is hung from the ceiling of a room by two massless strings. A uniform magnetic field is directed from the ceiling to the floor. When a current exists in the wire, the wire swings upward and makes an angle with respect to the vertical (wire is in equilibrium).
The wire has a length of 0.20 m and a mass of 0.065 kg and carries a current of 42 A. The magnitude of the magnetic field is 0.060 T.
(e) What is the algebraic expression for the angle in the drawing? Express your answer in terms of the current I in the wire, the length L of the wire, the magnitude B of the magnetic field, the mass m of the wire, and the magnitude g of the acceleration due to gravity.
Homework Equations
F = ILB sin(theta)
The Attempt at a Solution
While this is a relatively easy problem, I still can't see what mistake I am making.
First, given that the wire is in equilibrium,
The three forces acting on the wire in the question are Tension in the two
Strings, the magnetic force from the magnetic field acting on the wire, and the force of gravity.
Using right hand rule, the magnetic force points to the right. It has to be perpendicular to the magnetic field and current (current replacing the velocity component in the right hand rule)
Knowing this, three equations are generated:
2T = Tension of two strings
the tension can be resolved into x and y components
x-component = 2Tsin(theta)
y-component = 2Tcos(theta)
Magnetic Force = ILBsin(theta) going to the right
Force of Gravity = mg going down
using Netwon's second law,
2Tcos(theta) - mg = 0
2T = mg / (cos(theta)) // solving for 2T using y-components
2Tsin(theta) - ILBsin(theta) = 0
2Tsin(theta) = ILBsin(theta) // solving for theta
2T = ILB
mg / (cos(theta)) = ILB // substitution from previous equation
mg / ILB = cos(theta)
arccos( mg / ILB ) = theta
This is the answer I arrived at for question (e), but according to my online problem set this answer is incorrect. If any insight could be given that would be great. Thanks!
Last edited by a moderator: