reigner617
- 28
- 0
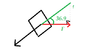
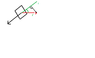
The Question: An ice block of mass M=80.0 kg is held stationary on a frictionless ramp. The ramp is at an angle of 36.9 degrees above the horizontal. If the block is held in place by a horizontal force directed horizontally toward the center of the block, find the magnitude of this force.
Related Equations: F = mgsinθ, F = mgcosθ
The Solution: Our professor solved it as follows:
Fcosθ = mgsinθ
F= mgsinθ/cosθ
= 470.7/ cos 36.9
= 588.6 NMy only confusion is to why he took this approach. I understand that when the force is tangential, we use mgsinθ; when the force is perpendicular, we use mgcosθ, but there doesn't seem to be a "formal" formula for a horizontal force
Related Equations: F = mgsinθ, F = mgcosθ
The Solution: Our professor solved it as follows:
Fcosθ = mgsinθ
F= mgsinθ/cosθ
= 470.7/ cos 36.9
= 588.6 NMy only confusion is to why he took this approach. I understand that when the force is tangential, we use mgsinθ; when the force is perpendicular, we use mgcosθ, but there doesn't seem to be a "formal" formula for a horizontal force