Force on Kneecap: Find Magnitude & Direction

[DavidDishere]

Homework Statement

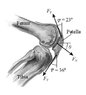
The figure shows the quadriceps
and the patellar tendons attached
to the patella (the kneecap). If the
tension FT in each tendon is
1.2 kN, what is (a) the magnitude and (b) the direction
of the contact force θ exerted on the patella by
the femur?

Homework Equations

FTsin θ + FTsin θ = FN (normal force)

c² = a² + b² - 2abcos θ

The Attempt at a Solution

I've tried using the above equation and got 1.1742 kN but that is basically assuming the normal force is horizontal right and there would be no angle?

I've also been playing around trying to make a triangle by moving the forces but my trig is a little rusty. I moved the lower FT up to the bottom of the top FT so that angle would be 59 degrees. Then FN would make the top of that upside down triangle. I could use the law of cosines and get 1.1818 kN. I know my sig figs aren't right but I'm just trying to show the difference. As a side note, we haven't ever used the law of cosines in class and it started out very basic and slow so I'm not sure its needed to solve this problem. I don't know how I would get the angle though.

 

[rl.bhat]

Fx = (FT*sinθ1 + FT*sinθ2) will give you horizontal component of the net force.
Fy = (FT*cosθ1 - FT*cosθ2) will give you vertical component of the net force.
Find the magnitude and direction of the resultant force.

 

[Delphi51]

The two tension forces must equal Fn. Just write out their components, horizontal and vertical. The horizontal one would be:
Tsin(23) + Tsin(36) = Fncos(θ)
Two equations, two unknowns so you can solve to find both Fn and θ.