shawli
- 77
- 0
Homework Statement
A skier on a slope inclined at 4.7 degrees to the horizontal pushes on ski poles and starts down the slope. The initial speed is 2.7 m/s. The coefficient of kinetic friction between skis and snow is 0.11. Determine how far the skier will slide before coming to rest.
Homework Equations
uK= 0.11
v initial= 2.7 m/s
v final= 0.0 m/s
Fk = uK*Fnormal
F=ma
(v final)^2 = (v initial)^2 +2*a*d
The Attempt at a Solution
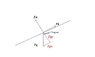
(Refer to system diagram for notations and stuff!)
So from what I can tell, the applied force is the horizontal component of gravity, Fgx, and the normal force is the vertical component of gravity, Fgy.
The horizontal component of gravity is:
Fgx= (sin4.7)(9.8)(m)
The force of kinetic friction would come out to be:
Fk=uK*Fgy
Fk=(0.11)(cos4.7)(9.8)(m)
The net force would be:
Fnet = Fapplied - Fkinetic
Fnet = Fgx - Fk
Fgx - Fk = m*a
So, solving, I get:
(sin4.7)(9.8)(m) - (0.11)(cos4.7)(9.8)(m) = m*a
a = 8.67 m/s^2
Now I can use acceleration to find the distance traveled by the skier:
(v final)^2 = (v initial)^2 +2*a*d
0 = (2.7)^2 +(2)(8.67)(d)
d= 0.42 m
The actual answer is 13m and I'm sure I've done something wrong
 .
.Can someone guide me through this, please?