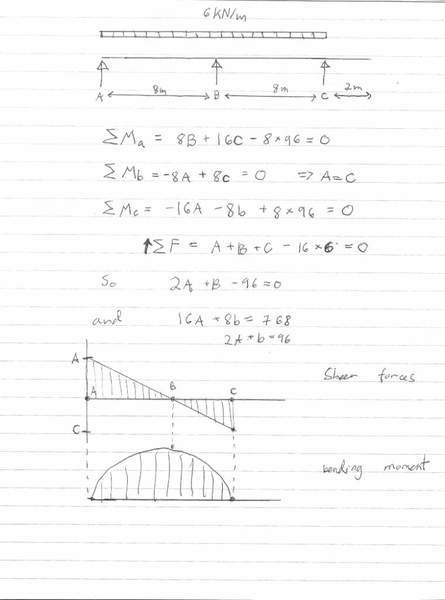
The discussion centers on solving a statically indeterminate beam problem, emphasizing that equilibrium equations alone are insufficient. Participants note that the shear and moment diagrams are incorrect due to the omission of the reaction force at point B. Various approaches to address the indeterminacy are suggested, including the use of the Force Method and superposition principles. The conversation also touches on the possibility of intuitive solutions for certain parts of the problem, particularly regarding deflected shapes and bending moment diagrams. Understanding the relationships between support types, loading, and deflection is highlighted as crucial for solving the problem effectively.