Forklift Stability: How Much Weight to Keep from Tipping?

[Ryank]

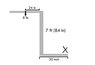
I understand that I will probably need to give some more variables here, but I am not sure what they are. in any case, my question to you all is this: As shown in the diagram below, realistically, how much weight should be placed at the x to keep this forklift from tipping over. I am working on a robot for the FRC competition and I'm trying to find out if the physics behind our design even make sense, a 7 ft forklift holding a 42 inch diameter 8 lb ball on a 30 inch long 28 inch wide base? It just doesn't sound right.

 

[FredGarvin]

I can't see the picture yet. However, the process you need to follow is to ensure that the vehicle's center of gravity stays within the footprint of its tires, treads, etc...

 

[Danger]

Welcome to PF, Ryan.
I don't know anything about this contest, so I'll just make a suggestion that might be in violation of the rules. As Fred pointed out, you need to keep your centre of gravity over the main body. How about turning the forks around, or tilting the hoist tower back, as soon as you pick up the load?

 

[LURCH]

One variable you will need to consider is the motion of the forklift; will it be stationary or will it drive around? If the forklift moves, then it will generate g-forces as it accelerates (decelerates). These are the forces that will cause it to tip over. I learned this the hard way.

 

[russ_watters]

In a static situation, you can simply ratio the weights and the distances, but as others said, when you start moving it, the motion comes into play.

 

[rbj]

In a static situation, you can simply ratio the weights and the distances, but as others said, when you start moving it, the motion comes into play.

i think you got to apply D'Alembert's principle in the case of decelleration. decellerating folklifts want to tip over toward the front. lotsa laffs when that happens.