SUMMARY
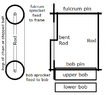
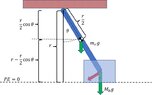
The discussion centers on the calculations required for a Four-Bar Parallel Linkage Pendulum system, specifically addressing the complexities of determining angular velocity and moments of inertia for rods AD and BC, which rotate around separate axes. The user seeks to calculate angular velocity based on potential and kinetic energy while considering the unique challenges posed by the crossing rods and their varying lengths. Key insights include the necessity of treating the system as a virtual rod for simplification and the importance of energy conservation principles in deriving angular velocity.
PREREQUISITES
- Understanding of potential and kinetic energy calculations in mechanical systems.
- Familiarity with moment of inertia and its application in rotational dynamics.
- Knowledge of the Parallel Axis Theorem for calculating moments of inertia.
- Basic principles of energy conservation in physics.
NEXT STEPS
- Research the application of the Parallel Axis Theorem in complex systems.
- Study energy conservation methods in mechanical systems, focusing on pendulums.
- Explore numerical methods for solving angular velocity in dynamic systems.
- Investigate literature on Four-Bar Linkage mechanisms and their dynamics.
USEFUL FOR
Mechanical engineers, physics students, and hobbyists involved in robotics or pendulum design who are looking to deepen their understanding of dynamic systems and energy calculations in linkage mechanisms.