- #1
Tanya Sharma
- 1,540
- 135
Homework Statement
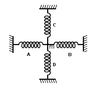
Figure shows a particle of mass m attached with four identical springs each of length L0. Initial tension in each spring is F0.Neglect gravity calculate the period of small oscillations of the particle along a line perpendicular to the plane of figure. (Take F0 = (0.01 π2)N, m = 100 gm, L0 = 10cm)
Homework Equations
The Attempt at a Solution
In the equilibrium state length of the spring L = L0 + z ,where L0 is the original length and z is the initial extension in the spring when in equilibrium.
Initial tension in each spring when in equilibrium = kz = F0
Suppose the mass is displaced by x amount upwards .In the attachment L' represents the new length.
L'=√(L2+x2)
Force by a spring = k(L'-L0) = = k(L'-L+z) = k(L'-L)+kz
This force will have a a horizontal component and a a vertical component .The horizontal component will be canceled by a similar component from the opposite string .
The net force from all four springs will be F = 4k(L'-L0 )sinθ = 4k(L'-L)sinθ + 4kzsinθ
sinθ = x/L'
So net force =4kx(L'-L)/L' + 4kxz/L’
=4kx(1-L/L') + 4kxz/L’
I somehow feel I am not approaching the problem correctly .
I would be grateful if somebody could help me with the problem.
Attachments
Last edited: