robertjford80
- 388
- 0
Homework Statement
The Attempt at a Solution
Obviously brackets mean something other than parentheses because .5[0 + 0] ≠ .5
The numbers in parentheses are, respectively, the usual definition of a Fourier series, and the formulas for the coefficients of the series.If a periodic function f(x) with period ##2\pi## is piecewise continuous in the interval ##-\pi \leq x \leq \pi## and has a left-and right-hand derivative at each point of that interval, then the corresponding Fourier series (7) [with coefficients (6)] is convergent. Its sum is f(x), except at a point x0 at which f(x) is discontinuous and the sum of the series is the average of the left- and right-hand limits of f(x) at x0.
robertjford80 said:
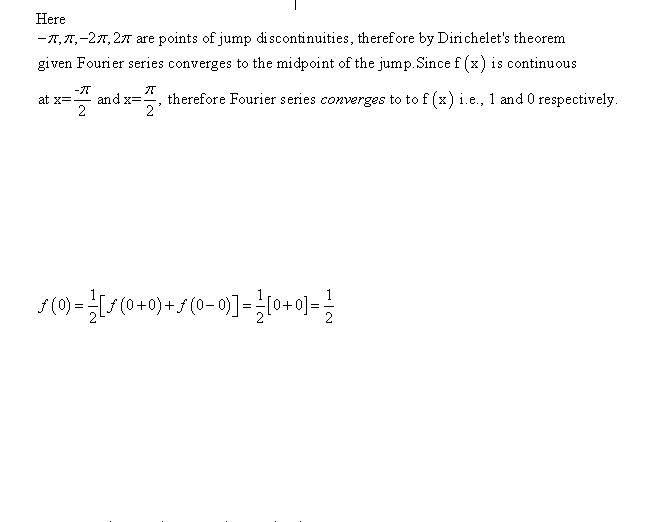
The Attempt at a Solution
Obviously brackets mean something other than parentheses because .5[0 + 0] ≠ .5