naspek
- 176
- 0
hey there.. i really don't know how to start answering this question.. can someone please guide me to solve this question..
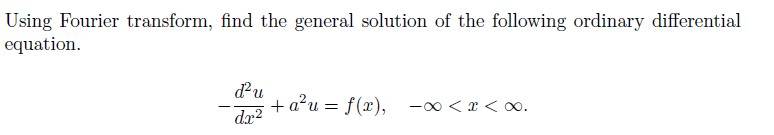
still blur...gabbagabbahey said:Since the question tells you to use Fourier transforms, you start by taking the FT of both sides of the differential equation...
gabbagabbahey said:When you take the Fourier transform of -\frac{d^2u}{dx^2} (That's what the F[\ldots] means) you get k^2F, or k^2\tilde{u}(k).
This gives you an algebraic (instead of differential) equation you can solve for \tilde{u}. To find u, you then take the inverse FT.
This is a very basic application of using FTs to solve DEs and I have a hard time believing that your textbook doesn't provide a similar example. You should really be in the habit of studying the relevant section of your text/notes before attempting homework problems that are based off of it.
naspek said:i've done the inverse..
F^-1[g^(k)] = g(x) = 1/ √2∏ ∫g^(k)e^ikx dk
........ = 1/ √2∏ ∫ 1/ (k^2 + a^2)e^ikx dk
......= √2∏ [(e^-a|x|) / 2a]
<br /> <br /> inverse both side...<br /> i get..<br /> <div class="bbImageWrapper js-lbImage" title="mathssss.jpg" data-src="https://www.physicsforums.com/attachments/mathssss-jpg.133258/" data-lb-sidebar-href="" data-lb-caption-extra-html="" data-single-image="1"> <img src="https://www.physicsforums.com/attachments/mathssss-jpg.133258/" data-url="" class="bbImage" data-zoom-target="1" style="" alt="mathssss.jpg" title="mathssss.jpg" width="472" height="79" loading="lazy" decoding="async" /> </div><br /> <br /> is that my general solution?gabbagabbahey said:That looks good, now use the composition rule to take the inverse FT of \hat{u}=\hat{g}\hat{f}[/itex]...
<br /> <br /> <blockquote data-attributes="" data-quote="gabbagabbahey" data-source="post: 2660196" class="bbCodeBlock bbCodeBlock--expandable bbCodeBlock--quote js-expandWatch"> <div class="bbCodeBlock-title"> gabbagabbahey said: </div> <div class="bbCodeBlock-content"> <div class="bbCodeBlock-expandContent js-expandContent "> Does \frac{1}{2a}\int f(x) e^{-a|x|}dx really represent the convolution of f and g? </div> </div> </blockquote><br /> by convolution theorem,<br /> F^−1{F*G} = f ·g <br /> correct?<br /> so, i just substitute it..?<br /> kinda confused <img src="https://cdn.jsdelivr.net/joypixels/assets/8.0/png/unicode/64/1f615.png" class="smilie smilie--emoji" loading="lazy" width="64" height="64" alt=":confused:" title="Confused :confused:" data-smilie="5"data-shortname=":confused:" />gabbagabbahey said:That looks good, now use the composition rule to take the inverse FT of \hat{u}=\hat{g}\hat{f}[/itex]...
gabbagabbahey said:That's better!
However, that's just part of the general solution. You can also add any function, u_h, which satisfies the corresponding homogeneous ODE, -\frac{d^2 u_h}{dx^2}+a^2u_h=0, to the u(x) you've found, and the result will still satisfy your ODE. So, you need to find that homogeneous solution and add it to what you've found above in order to obtain the true general solution.
gabbagabbahey said:First worry about finding the homogeneous part of the general solution. Solve the Homogeneous equation.
naspek said:is this my general solution?
<br /> y(x)=\frac{1}{\sqrt{2\pi}}\frac{1}{a}\sqrt{\frac{\pi}{a}}\int_{-\infty}^{\infty} e^{-a|x|}f(x-t)dt<br />
fuuhh! (just for a moment..)gabbagabbahey said:Yup!
gabbagabbahey said:Are you asked to solve it? Or are you only asked to show that a solution exists? If it's the latter option, just show that the integral converges.
so.. i need to test the equations below?gabbagabbahey said:You want to test to see if y(x) converges for each of your two f(x)'s. If the integral doesn't converge, then no solution exists.
gabbagabbahey said:You want to test to see if y(x) converges for each of your two f(x)'s. If the integral doesn't converge, then no solution exists.
gabbagabbahey said:I just noticed that you have an error in your expression. Convolution tells you that y(x)=\frac{1}{2a}\int_{-\infty}^{\infty}f(x-t)e^{-a|t|}dt, not \frac{1}{2a}\int_{-\infty}^{\infty}f(x-t)e^{-a|x|}dt.