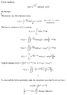You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Fourier Transform Tricky Integral
- Thread starter michaelbarret
- Start date
Physics news on Phys.org
chiro
Homework Helper
- 4,817
- 134
michaelbarret said:Hi I am trying to analytically calculate the Fourier transform attached.
I am getting really stuck with the integral, can anyone help?
I've attached how far I've got with it, any help much appreciated!
Kind Regards,
Mike
Hey michaelbarret and welcome to the forums.
Hint: Use the subsitution and try integration by parts twice and see what you get.
HallsofIvy
Science Advisor
Homework Helper
- 42,895
- 984
The only thing complicated about that integral is your way of doing it. Instead, do it by parts:
\int cos(\omega x)e^{ax}dx
Let u= cos(\omega x, dv= e^{ax}dx so that du= -\omega sin(\omega x)dx and v= (1/a)e^{ax} so we have
\int udv= uv- \int vdu= \frac{1}{a}e^{ax}cos(\omega x)+ \frac{\omega}{a}\int e^{ax}sin(\omega x)dx
Now, do it again. Let u= sin(\omega x) and dv= e^{ax} so that du= \omega cos(\omega x)dx and v= (1/a) e^{ax}.
Now you have
\int e^{ax}cos(\omega x) dx= \frac{1}{a}e^{ax}cos(\omega x)+\frac{\omega}{a^2}e^{ax}sin(\omega x)- \frac{\omega^2}{a^2}\int e^{ax}cos(\omega x)dx
Add \int e^{ax}cos(\omega x) dx to both sides and divide by 2.
\int cos(\omega x)e^{ax}dx
Let u= cos(\omega x, dv= e^{ax}dx so that du= -\omega sin(\omega x)dx and v= (1/a)e^{ax} so we have
\int udv= uv- \int vdu= \frac{1}{a}e^{ax}cos(\omega x)+ \frac{\omega}{a}\int e^{ax}sin(\omega x)dx
Now, do it again. Let u= sin(\omega x) and dv= e^{ax} so that du= \omega cos(\omega x)dx and v= (1/a) e^{ax}.
Now you have
\int e^{ax}cos(\omega x) dx= \frac{1}{a}e^{ax}cos(\omega x)+\frac{\omega}{a^2}e^{ax}sin(\omega x)- \frac{\omega^2}{a^2}\int e^{ax}cos(\omega x)dx
Add \int e^{ax}cos(\omega x) dx to both sides and divide by 2.
michaelbarret
- 2
- 0
Thanks HallsofIvy for your reply.
I think the biggest thing I'm unsure on is how my original signal can be generalised to ∫cos(wx) e^ax dx. In my case does w=w, x=t(1-qt) and dx=dt?
Also sorry If it's obvious but I don't really understand why I should add ∫e^ax cos(ωx)dx to both sides and divide by 2.
I can't figure out how to integrate the complex exponential associated with the FT either, ∫e^-jwt dt
I think the biggest thing I'm unsure on is how my original signal can be generalised to ∫cos(wx) e^ax dx. In my case does w=w, x=t(1-qt) and dx=dt?
Also sorry If it's obvious but I don't really understand why I should add ∫e^ax cos(ωx)dx to both sides and divide by 2.
I can't figure out how to integrate the complex exponential associated with the FT either, ∫e^-jwt dt
algebrat
- 428
- 1
Yeah last helper might not have noticed the squaring of t in the original problem, it also looks like you didn't write it after the first line. But it looks like you were close to done, I like what you have worked out on the PDF. I think the next goal might be to complete the square and use some substitutions and move things around so you almost have that thing that's equal to root pi over a.
Last edited:
I'm reviewing Meirovitch's "Methods of Analytical Dynamics," and I don't understand the commutation of the derivative from r to dr:
$$
\mathbf{F} \cdot d\mathbf{r} = m \ddot{\mathbf{r}} \cdot d\mathbf{r} = m\mathbf{\dot{r}} \cdot d\mathbf{\dot{r}}
$$
Similar threads
- Replies
- 12
- Views
- 11K
- Replies
- 2
- Views
- 2K
- Replies
- 3
- Views
- 10K
- Replies
- 5
- Views
- 2K
- Replies
- 3
- Views
- 2K
- Replies
- 7
- Views
- 3K
- Replies
- 9
- Views
- 2K
- Replies
- 2
- Views
- 2K
- Replies
- 13
- Views
- 3K
- Replies
- 3
- Views
- 2K
Hot Threads
-
I Harmonic series Ʃ1/n diverges but p-series Ʃ(1/n)^p diverges?
- Started by Dimwitted_UniStudent
- Replies: 4
- Calculus
Recent Insights
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 7
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 0
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 1
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 7
- General Math
-
Insights Fermat's Last Theorem
- Started by fresh_42
- Replies: 91
- General Math
-
Insights Why Vector Spaces Explain The World: A Historical Perspective
- Started by fresh_42
- Replies: 0
- General Math