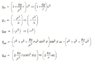Frame Dragging & Galactic Rotation: Implications for AGN & Black Holes

[mysearch]

Hi,
I am interested in the issue of frame dragging used in a number of galactic rotation models. However, I wanted to first make sure that I have a better understanding the relativistic implications of frame dragging. While the issue of galactic rotation is not the subject of this thread, it is possibly useful to mention that the standard galactic model appears to assume a central black surrounded by a accretion layer, which is often collectively described as the active galactic nucleus (AGN) from which the typical spiral arms extend. Now the only point of this detail is to highlight that AGN appear to extend out many 1000’s of times beyond the Schwarzschild radius [Rs] of the black hole (BH). If so, then it is assumed that the relativistic effects in terms of both velocity and gravitation within the spiral arms may be minimal. Therefore, in the current context, the following PF discussions are only provided as a general cross reference:

PF frame dragging reference
black holes, frame dragging and the effect on gravity

While many discussion of frame dragging are anchored in the Kerr metric of a rotating black hole, it seems that the angular velocity of the dragged frame can be presented in the following form, although this assumption may be incorrect:

[1] $\omega_D = k \left( \frac{G}{c^2} \right) \left( \frac{M \omega_{(BH)}}{R} \right)$

The parameter [k] is often described in terms of some density distribution, which I think Lense-Thirring originally quantified as 4/3 for a spherical distribution, which might not be applicable for a disk galaxy. The [G/c^2] is the gravitation constant and speed of light that essentially act as a conversion factor for MKS units. The parameter [M] is assumed to be the mass of the central black hole rotating at an angular velocity [w]. For the purpose of approximate calculations, the mass [M] of a galactic black hole can be estimate in millions of solar masses, which then determines the radius [Rs]:

[2] $Rs = \frac{2GM}{c^2}$

Again, the angular velocity [w] of the black hole itself can be estimated by calculating the circumference and dividing by a maximum tangential velocity up to [0.99c]; although the actual figure is not directly relevant at this stage. Therefore, it would seem that the frame dragging angular velocity is inversely proportional to the distance [R] from the BH. However, in order to convert the frame drag angular velocity into a linear tangential velocity, it is assumed that the relationship [w=v/r] applies, such that [1] would appear to become:

[3] $v_D = k \left( \frac{G}{c^2} \right) \left(M \omega_{(BH)} \right)$


While [3] seem right and aligns to the correct units of velocity, i.e. m/s, the implication appears to be that this tangential drag velocity will remain constant irrespective of distance!

So my first question is whether this is right?

My second issue is really predicated on the answer to the question above, but on the assumption that the extreme relativistic effects of the BH do not extend out beyond the AGN, then a stable orbit would only require a classical rotational velocity to counteract the pull of gravity, i.e.

[4] $F= \frac{mv_O^2}{r}= \frac{GMm}{r^2}$

Re-arranging, this velocity falls with the inverse square-root of distance:

[5] $v_O=\sqrt{ \frac{GM}{r}}$

The implication of [3] and [5], as they stand, seems to suggest that the constancy of the frame dragging velocity in [3] must eventually exceed the orbital velocity in [5], such that it would sweep stars within the spiral arm to ever greater distance. Something seems intuitively wrong with this description, but I am not sure where and would therefore appreciate any clarifications or insights. Thanks.

 

[Bill_K]

Both the references you quote and Wikipedia's article on frame dragging state that the angular speed of frame dragging in a weak gravitational field is Ω = - g_tφ/g_φφ which falls off as r^-3.

 

[Bill_K]

Another way to see the frame dragging effect is to look at the particle orbits. If you do this for the Kerr metric, you find the angular velocity necessary to maintain a circular orbit in the equatorial plane is given by M(1 - aω)² = r³ω² where M is the geometrized Schwarzschild mass and a is the Kerr parameter. Note that for a = 0 this reduces to ω = ± √(M/r³). (Interesting fact that this is the same as for a Newtonian orbit.)

For a ≠ 0 it's a quadratic equation for ω with the solution

ω = (-Ma ± √(Mr³))/(r³ - Ma²)

Frame dragging reveals itself by the fact that the angular velocity necessary for a circular orbit is different depending on whether you're going clockwise or counterclockwise. Another way of putting it is that both orbits rotate counterclockwise with an additional angular velocity -Ma/(r³ - Ma²).

 

[mysearch]

Both the references you quote and Wikipedia's article on frame dragging state that the angular speed of frame dragging in a weak gravitational field is Ω = - g_tφ/g_φφ which falls off as r^-3.

Bill: many thanks for the steer. With regards to the ‘PF frame dragging’ reference, I had originally ‘morphed’ the weak-field frame-dragging equation below to be equivalent to my equation [1] as follows based on the assumption of a circular path. At face value this looked OK, but clearly leads to the wrong result based on your coefficient formulation.

$\omega_D = \frac{2GJ}{c^2 r^3}$

$\omega_D = \frac{2G}{c^2} \frac{J}{r^3}$

$\omega_D = \frac{2G}{c^2} \frac{mvr}{r^3}$

$\omega_D = \frac{2G}{c^2} \frac{m (\omega r) r}{r^3}$

$\omega_D = \frac{2G}{c^2} \frac{m \omega}{r}$

So I have started to look at the coefficient solution you’ve indicated, i.e. Ω=-g_tφ/g_φφ based on the Kerr metric, which seems to suggest a more complex solution, but which then suggests that the angular velocity does fall of faster than [1/r], such that tangential velocity also falls off as some inverse function of [r], which seems intuitively better. However, I will try to plot some results in a spreadsheet to get a better feel of the change. The attachment shows all the Kerr coefficients I plan on using just by way of a cross check and then simplified to an equatorial plane. Thanks again.

 

[mysearch]

Bill,
Just a quick note to say that my last response crossed with your 2nd post. I am now looking at the Kerr metric solutions and, as stated, will try to plot some results to get a better idea of what is going on. However, one of the reasons why I was not looking at the Kerr metric is because one of the galactic models I was looking at rejected the Kerr metric on the ground that it was non-Machian. I am not really sure of the implications of this statement other than the Kerr metric possibly assumes an infinite boundary with no mass, while the alternative model is possibly looking for a finite boundary within an infinite universe. Thanks again.

 

[mysearch]

I am not sure that anybody will necessarily be interested in the following review of the Kerr metric related to frame dragging, but I thought I would post my results as a future point of reference and with the hope that somebody might correct any errors or misunderstanding. In posts 2 & 3, Bill_K responded to the OP regarding the equation for the frame dragging angular velocity and while I will comment on the solution based on the Kerr metric coefficients below, the status of following equations, touched on in post 4, is still somewhat unclear to me:

[1] $\omega_D = \frac{2GJ}{c^2 r^3} \Rightarrow k\frac{G}{c^2} \frac{M \omega_{(BH)}}{r}$

In [1], [M] is assumed to be the physical mass [kg] of the black hole, although the radius in which this mass exist appears to require some qualification – see [7] below. The angular velocity of the black hole $\omega_{BH}$ also needs some explaining, but various references suggest that the BH can spin up to speed approaching the speed of light [c]. So if the form on the left of [1], as taken from ‘PF frame dragging’, is valid, then surely so is the form on the right? If so, then frame dragging $[ \omega_D]$ would appear to be proportional to [1/r], if all other parameters were effectively constant, although in light of the Kerr metric solution, it is not clear whether [k] may also vary as a function of [r]. Anyway, based on post 2, there would appear to a more rigorous relativistic solution based on the ‘Kerr metric’ where the Wikipedia link provide the basic definitions. However, the form of the Kerr metric and the coefficients can be much simplified if only circular solutions in the equatorial plane are considered, e.g.

[2] $\omega_D= g_{\phi t}/ g_{\theta \theta}$

[3] $g_{\phi t} =2 \frac{Rs}{r} \alpha c$

[4] $g_{\theta \theta} = r^2+ \alpha^2 + \frac{Rs}{r} \alpha^2$

From the perspective of doing calculations and understanding the physical quantities involved, I prefer not to use geometric units. In this context, the Schwarzschild radius [Rs] is defined by:

[5] $Rs= \frac{2GM}{c^2}$

Now in post 4, Bill references a number of equations in terms of [M], where this quantity is actually the geometric mass with the units of metres, which I believe can be explained as follows:

[6] $M_{geo}= M \left( \frac{G}{c^2} \right)=metres$

Now the main purpose for highlighting [5] and [6] is to help physically interpret some of the variables in [3] and [4]. Comparing [5] and [6] suggests that the geometric mass is actually a measure of distance, which can be related to [Rs]:

[7] $M_g = \frac{Rs}{2}$

Before comments on the implications of [7], it might be worth defining the [α] variable used in [3] and [4]:

[8] $\alpha = \frac{J}{Mc} = \frac{Mvr}{Mc}= \frac{v}{c}r$

The angular momentum [J] is said to be a conserved property of a BH, such that as the original spinning star collapses into a BH with an ever decreasing radius, the rate of spin has to increase and can approach [c]. Now in [8], the variable [M] is the physical mass in [kg], but in order to quantify the extreme case [J=Mcr], it would seem that we need to associated the mass [M] of the BH with some form of radius. While I am not certain of the following assumption, it is suggested that [7] can be used to define this radius, such that [8] becomes:

[9] $\alpha = \left( \frac{v}{c} \right) \frac{Rs}{2}$

As such, [9] has the units of metres, which is consistent with its use in the Kerr metric and allows an extreme example of frame dragging to be formulated, where in term of some galactic BH, [M] might be defined as 1 million of solar masses, which then allows [Rs] to be determined. While the actual rotation speed of a BH is not really known, we might simply be assumed that the extreme case is so close to [c] that [v/c] in [9] is essentially unity. So based on the all the simplifying assumptions, e.g. equatorial solution and an extreme BH, we can present the ratio of the coefficient in [2] said to defined the frame dragging around a rotating BH as described by the Kerr metric in the following reduced form:

[10] $g_{\phi t} =2 \frac{Rs}{r} \frac{Rs}{2} c = \frac{Rs^2}{r}c$

[11] $g_{\theta \theta} = r^2+ \left( \frac{Rs}{2} \right)^2 + \frac{Rs}{r} \left( \frac{Rs}{2} \right)^2$

If I have got this right, the form of [2] for the extreme case being outlined becomes:

[12] $\frac{ g_{\phi t} }{ g_{\theta \theta} } = \omega_D = \frac{ c Rs^2}{ r^3+ \frac{rRs^2}{4} + \frac{Rs^3}{4r} }$

The results of [12] are shown in the attachment, which unlike [1] appears to show both the angular and tangential velocities fall with radius [r]. I am assuming that the significant difference between [1] and [12] is the rate of change of $[d(\omega_D)/dr]$ is now presumably dominated by the denominator variable $[1/r^3]$. However, I will leave it there for now to see whether anybody objects to any of the assumption or results that have been a bit rushed and need to be double checked. Thanks

 

[mysearch]

By way of a footnote and correction to some of the issues raised in this thread, which started after reading a paper on viscosity and the idea of frictional drag. The units of the coefficient of viscosity are defined as follows:

[1] $\eta = \frac{kg}{ms} \Rightarrow \frac{m \omega}{r}$

As such, I thought this idea might also be relevant to the concept of inertial drag around a black hole, which led to the formulation cited in post 1, i.e.

[2] $\omega_? = k \left( \frac{G}{c^2} \right) \left( \frac{m \omega}{R} \right)$

On initial cross checking, I thought this equation could be equated to the weak field frame dragging equation given in the link ‘PF frame dragging’, which I now believe is a source of error:

[3] $\omega_D = \frac{2GJ}{c^2 r^3}$

The ‘morphing’ of [3] into [2], as outlined in post 4, confused two different radii [r, R] linked with the radius of the dragging effect [r] and the radius of the angular momentum [J] of the black hole. As such, the following morphing seems to be more appropriate.

[4] $\omega_D = \frac{2G}{c^2} \frac{J}{r^3}$

[5] $\omega_D = \frac{2G}{c^2} \frac{Mv_{BH}R}{r^3}$

[6] $\omega_D = \frac{2G}{c^2} \frac{M (\omega_{BH} R) R}{r^3}$

[7] $\omega_D = \frac{2GM}{c^2} \frac{\omega_{BH}R^2}{r^3} = Rs \frac{\omega_{BH}R^2}{r^3}$

The form of [7] now seems to reflect the basic form of the Kerr solution given in post 6/[12]. In terms of any drag effect in the spiral arms of a galaxy, where [r>>R], then [7] above would now appear to converge to the weak field form of [3]. Although quantifying the angular momentum of the BH to some radius [R=Rs/2], see post 6, when [J] extends out into the surrounding spacetime possibly still needs some clarification/correction.

 

[pervect]

I am not sure that anybody will necessarily be interested in the following review of the Kerr metric related to frame dragging, but I thought I would post my results as a future point of reference and with the hope that somebody might correct any errors or misunderstanding. In posts 2 & 3, Bill_K responded to the OP regarding the equation for the frame dragging angular velocity and while I will comment on the solution based on the Kerr metric coefficients below, the status of following equations, touched on in post 4, is still somewhat unclear to me:

[1] $\omega_D = \frac{2GJ}{c^2 r^3} \Rightarrow k\frac{G}{c^2} \frac{M \omega_{(BH)}}{r}$

In [1], [M] is assumed to be the physical mass [kg] of the black hole,

I'm afraid I didn't get very far in looking this over. In fact, this is as far as I got :(. There are not really a zillion sorts of mass in General Relativity , but with over 4 it seems like it sometimes. However, none of them are called "physical mass". So I"m at a bit of a loss already for which one you might be thinking of here - and why you'd regard it as being "physical".

If I had a better idea of what you were doing, maybe I could guess which one you meant - at the moment, I don't though.

Overall, it seems to me that you're trying to interpret GR results in Newtonian terms using Newtonian language. This strikes me as a recipe for severe confusion at best.

Reading on a bit "the angular velocity of the black hole" seems like another good/bad example of somethign that really doesn't make a lot of sense, like someone trying to use a Newtonian mindset beyond where it's applicable.

 

[mysearch]

I suspect from the tone of your comments that any explanation on my part will probably not help, but here goes.

I'm afraid I didn't get very far in looking this over. In fact, this is as far as I got :(. There are not really a zillion sorts of mass in General Relativity , but with over 4 it seems like it sometimes. However, none of them are called "physical mass". So I"m at a bit of a loss already for which one you might be thinking of here - and why you'd regard it as being "physical".

In post 3, Bill_K introduced the term ‘geometrized Schwarzschild mass’ that many GR texts also make reference based on the use of geometric or natural units, where [G=c=1]. As stated, in order to do basic calculations and infer some ‘physical’ interpretation to the description I prefer not to use these units. In the specific instance you cite regarding ‘physical mass’ I was making reference to the fact that the mass associated with a BH is often described as a physical star with mass [kg] that collapse on itself to which angular momentum [J] might be associated. So, in the context used, physical simply meant kilograms not metres.

If I had a better idea of what you were doing, maybe I could guess which one you meant - at the moment, I don't though. Overall, it seems to me that you're trying to interpret GR results in Newtonian terms using Newtonian language. This strikes me as a recipe for severe confusion at best.

One of the issues I was trying to resolve for myself related to how the angular momentum might be quantified in terms of the BH, e.g. J=mvr. While this is indeed a simple classical approximation, I was trying to understand a description of a BH spinning at near light speed, i.e. what is spinning and at what radius. So what I was trying to do was to get a better idea of the underlying physics of frame dragging. Based on Bill_K response, I reviewed the Kerr metric, a GR solution, which made me question the error in my original frame dragging equation – see post-1/equation [1]. In post 7, I was trying to pointing out the source of the error, which seems to be related to the interpretation of the angular momentum of the BH at some defined radius [Rs/2].

Reading on a bit "the angular velocity of the black hole" seems like another good/bad example of somethign that really doesn't make a lot of sense, like someone trying to use a Newtonian mindset beyond where it's applicable.

Fair enough. While I have tried to explain myself, I suspect that it is probably not worth either of us wasting any more time on what appears to be fruitless exchanges.