Free Body Diagram Help: Learn How to Draw It

Click For Summary

Homework Help Overview

The discussion revolves around drawing a free body diagram related to a physics problem involving multiple masses and forces. Participants are seeking clarification on how to represent the forces acting on specific bodies within the system.

Discussion Character

  • Exploratory, Assumption checking, Problem interpretation

Approaches and Questions Raised

  • Participants inquire about which specific body should be represented in the free body diagram, with mentions of different masses and points in the system. There is also a discussion about the forces acting at a particular junction, including horizontal and vertical components.

Discussion Status

The conversation is ongoing, with participants providing insights into the forces involved and seeking further clarification on the setup. Some guidance has been offered regarding the forces acting at a specific point, but there is no clear consensus on the diagram's representation yet.

Contextual Notes

Participants are working under the constraints of a homework assignment, which may limit the information available for discussion. There is an emphasis on understanding the forces involved without providing a complete solution.

bobmarly12345
Messages
26
Reaction score
0

Homework Statement


can anyone show me what the free body diagram of this would look like?
Thankyou
 

Attachments

  • P10001053.jpg
    P10001053.jpg
    22.6 KB · Views: 468
Physics news on Phys.org
bobmarly12345 said:

Homework Statement


can anyone show me what the free body diagram of this would look like?
Thank you
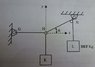
For which body do you want the Free Body Diagram? ... mass K, mass L, the pulley at N, or the junction of the cables at H
 
well the question asks me to work out the mass of K
 
There are three forces acting at H. First there is a horizontal force acting toward point G. Second, there is a vertical force due to the weight of K. Third there is a force toward point N. The magnitude of the downward force is, of course, mg. The magnitude of the force toward N is the same as the weight of the mass at L. Decompose the force toward N into its horizontal and vertical components.
 

Similar threads

Why are moments not included in free body diagrams?
  • · Replies 31 ·
2
Replies
31
Views
2K
Undergrad Force Generated By Leg Muscles in Free Body Diagrams
  • · Replies 8 ·
Replies
8
Views
2K
Potential Mistake in Free-Body Diagram
  • · Replies 5 ·
Replies
5
Views
2K
Undergrad Can free body diagrams be used if friction at pivot is not negligible?
  • · Replies 3 ·
Replies
3
Views
1K
Distributed weight of inclined beam.
  • · Replies 11 ·
Replies
11
Views
3K
Is it friction or tension acting on the person hanging on a rope?
  • · Replies 4 ·
Replies
4
Views
1K
High School Elevator Question -- What does a downward acceleration mean?
  • · Replies 4 ·
Replies
4
Views
2K
Beam boundary condition problem
  • · Replies 12 ·
Replies
12
Views
3K
Solving Free-Body Diagrams for Moving Nuts on Rods: Tips and Techniques
  • · Replies 9 ·
Replies
9
Views
2K
When are reactive forces enough to support this body?
  • · Replies 14 ·
Replies
14
Views
2K