Nicholas Tok
- 3
- 0
Hi guys,
I am trying to do this question on my own but i am not confident if what i am doing is correct. please download the Question2.docx file and my workings are in blue. hope someone can help me with this.
1. Homework Statement
A. For circuit (a) below, calculate:
R_e and R_C to make I_C≈0.2 mA and V_CE≈6V.
C_e to give a pole frequency at about 400 Hz, and C_C to give a pole at about 50 Hz.
The oscilloscope input resistance is 1 MΩ. For initial calculations assume C_μ= 5pF and C_(CRO + cable)= 110 pF. (These will be measured in the lab.) The generator resistance is 50Ω, which may be taken as a good approximation to zero for this experiment. Moreover, the input will be monitored across the generator and its voltage kept constant, so it may be treated as an ideal voltage source.
Estimate the voltage gain, the frequency of the zero introduced by C_e, and the upper 3-dB frequency f_h. What is the voltage gain if C_e is omitted?
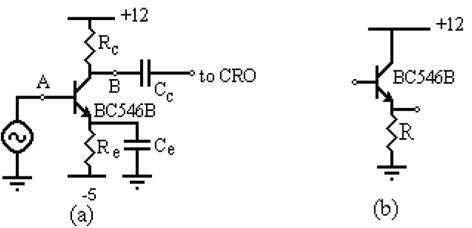
B. Circuit (b) is to be inserted in series at point B to buffer the load capacitance. Calculate R to give a collector current of about 1.2 mA. Assuming a 'typical' value for h_fe, recalculate f_h. Is the pole frequency introduced by C_C significantly affected?
C. Leaving circuit (b) in place, a 10 kΩ resistor is inserted at point A (simulating a higher source resistance than that of the generator). Recalculate f_h. Is the pole frequency introduced by C_e affected?
Question 2.docx
I am trying to do this question on my own but i am not confident if what i am doing is correct. please download the Question2.docx file and my workings are in blue. hope someone can help me with this.
1. Homework Statement
A. For circuit (a) below, calculate:
R_e and R_C to make I_C≈0.2 mA and V_CE≈6V.
C_e to give a pole frequency at about 400 Hz, and C_C to give a pole at about 50 Hz.
The oscilloscope input resistance is 1 MΩ. For initial calculations assume C_μ= 5pF and C_(CRO + cable)= 110 pF. (These will be measured in the lab.) The generator resistance is 50Ω, which may be taken as a good approximation to zero for this experiment. Moreover, the input will be monitored across the generator and its voltage kept constant, so it may be treated as an ideal voltage source.
Estimate the voltage gain, the frequency of the zero introduced by C_e, and the upper 3-dB frequency f_h. What is the voltage gain if C_e is omitted?
B. Circuit (b) is to be inserted in series at point B to buffer the load capacitance. Calculate R to give a collector current of about 1.2 mA. Assuming a 'typical' value for h_fe, recalculate f_h. Is the pole frequency introduced by C_C significantly affected?
C. Leaving circuit (b) in place, a 10 kΩ resistor is inserted at point A (simulating a higher source resistance than that of the generator). Recalculate f_h. Is the pole frequency introduced by C_e affected?
The Attempt at a Solution
Question 2.docx