Frictional forces between ropes

[tcd89]

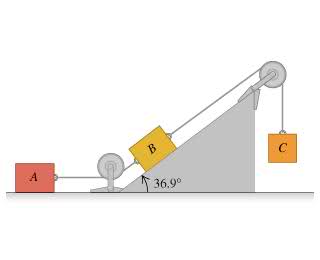
Blocks A, B, and C are placed as in the figure (Intro 1 figure) and connected by ropes of negligible mass. Both A and B weigh 23.2 N each, and the coefficient of kinetic friction between each block and the surface is 0.31. Block C descends with constant velocity.
Find the tension in the rope connecting blocks A and B.
What is the weight of block C?
If the rope connecting A and B were cut, what would be the acceleration of C?

$$\sum$$F_x=T₁sin36.9-$$\mu$$
$$\sum$$F_y=T₁cos36.9-w

I tried to find the tension between A and B, but it turned out wrong. I think there is something wrong with the equation I used. =/
And I'm completely at a lost as to how you answer the other two questions.
Help is appreciated! Thanks! =)

 

[LowlyPion]

Welcome to PF.

For the first question the key is that it is moving at constant velocity. Hence Ma is only being pulled with Tension that equals the frictional force retarding it which will be μ*Ma*g isn't it?

If you cut the rope, then that force would then be available to accelerate both blocks wouldn't it?