- #31
naviakam
- 103
- 3
What would be type of the potential responsible for the following equation:
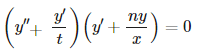
Last edited:
From solution to mother equation
- Thread starter naviakam
- Start date
Click For Summary
The discussion revolves around two equations: a power equation and an exponential equation, both related to ion spectra from a capacitor discharge experiment. Participants explore the possibility of deriving a "mother equation" that encompasses both forms, suggesting differentiation and analysis of their behavior in a vector field. The conversation highlights the need to correlate these equations with the underlying physical potential governing the ion acceleration. Concerns are raised about the appropriateness of the equations derived from curve fitting and the necessity of understanding the physics behind the data. Ultimately, the discussion emphasizes the importance of linking mathematical models to physical principles in experimental contexts.
- #32
- 42,783
- 10,488
In post #18 you let slip the crucial fact that your equations in post #1 come from attempts to fit data to readings. From then it was clear that attempting to find an equation that merged them over the whole range of x, as in posts up to that point, were a wild goose chase. Ignore all posts before #18.naviakam said:
Presumably what you have is a plotted curve that looks exponential over one part of the range and polynomial over another part. If so, there is probably no way to merge them into a single analytic expression.
E.g. consider a velocity/time graph for an object falling into water. There is no way to merge the equation for before hitting the water with the the one for after into a single analytic equation.
If my presumption is incorrect then please explain in detail what the situation is. Your response to @Fred Wright in post #30 sheds very little light on how you got your data.
- #33
naviakam
- 103
- 3
haruspex said:
capacitor discharge in a gas produces ions. these ions are measured by magnetic spectrometry in which particles pass through the magnet and curve according to their energy and form tracks on a plastic plate.
from magnetic spectrometry two types of ion spectra are obtained (not from a single discharge but from two separate discharges). the initial condition is similar for both discharges but two different spectrum are produced: one fits with power and the other with exponential fit.
what I am looking for is to guess the corresponding potential responsible for such spectra!
- #34
- 42,783
- 10,488
What is the difference?naviakam said:
You wrote that y is a number of ions and x is an energy. Does that mean y of the ions have energy x? If so, is that as a histogram, i.e. y is a count of ions in some energy range around x?
Just how good is the fit? How many datapoints? What value of n do you get?naviakam said:
Can you post the data in machine-readable form?
- #35
naviakam
- 103
- 3
haruspex said:
- #36
- 42,783
- 10,488
Ok, so y is the log of the intensity?naviakam said:
As I asked, what is the power (n) in that fit, and what is the difference between the two runs?
- #37
naviakam
- 103
- 3
haruspex said:
1. yes y is the number of ions.
2. n=4
3. the difference is the gas pressure in which the capacitor discharges:
at 6mbar the spectrum fits with exp
at 10mbar it's a power fit
- #38
- 42,783
- 10,488
The "power fit" graph you posted is log-linear, so is y in the power equation the number of ions (intensity?) or the log of the number?naviakam said:
And does this mean your exponential graph is also after taking logs, so you really have log(intensity) is negative exponential?!
Exactly?naviakam said:
So the full story is y=y(x,p), where p is the gas pressure.naviakam said:
Extremely artificially, you could write
##y=P(p)y_1(x)+(1-P(p))y_2(x)##, where P(6mbar)=0 and P(10mbar)=1.
I'm not seriously suggesting that would be valid, but you get the idea.
Last edited:
- #39
naviakam
- 103
- 3
haruspex said:
1. it's been plotted in log format, y is number only not log
2. 3.8<n<4.1
3. then what is the estimated potential leading to each term in the equation ##y=P(p)y_1(x)+(1-P(p))y_2(x)##?
- #40
- 42,783
- 10,488
Why would you plot it log-linear if trying to demonstrate a power law fit? Plot y-y0 log-log against x, or plot y-y0 against ##x^{-4}##.naviakam said:
As I wrote, I am not seriously suggesting that is the correct form. I was just showing you how, given a function of two variables, the dependence on one might look very different for a different value of the other. To get any reliable sense of what is going on you would need results for several intermediate values of the pressure.naviakam said:
Anyway, what is this potential you are asking about? The voltage on the capacitor? Some potential function?
- #41
naviakam
- 103
- 3
haruspex said:
I was wondering if from the spectra we can guess a general potential function for each of the following equations:
Last edited:
- #42
- 42,783
- 10,488
As I indicated, I don't know what you mean by a "potential function" in this context.naviakam said:
Perhaps you could illustrate by starting from the other end: pick some example of such a function and show what y=f(x,p), or differential equation, it would lead to.
Also, please post your "power fit" data as a graph of ln(y-y0) against ln(x).
- #43
naviakam
- 103
- 3
haruspex said:
1. the capacitor discharge voltage is 10 kV, but ions are accelerated to MeV by an unknown potential. Then we try to guess this accelerating potential (starting from the other side: from spectra to potential!).
2. " pick some example of such a function and show what y=f(x,p), or differential equation, it would lead to. "
Would you please help me how to do this.
3. here is the raw data:
1026.35 2.12E+10
973.90 2.28E+10
925.86 2.53E+10
881.75 2.73E+10
841.16 3.43E+10
803.73 4.18E+10
769.15 5.28E+10
737.15 6.57E+10
707.47 8.61E+10
679.92 1.15E+11
654.29 1.42E+11
630.42 1.89E+11
608.16 2.57E+11
587.38 3.53E+11
567.95 4.66E+11
549.77 6.18E+11
532.74 8.32E+11
516.77 1.10E+12
501.78 1.52E+12
487.70 1.90E+12
474.47 2.60E+12
462.02 3.33E+12
- #44
- 42,783
- 10,488
Are these the data that you claim a power law for?naviakam said:
For those data I get a decent straight line fit between ln(I) and V. Just a bit of a curve at one end. Looks like I is proportional to exp(-0.02V).
If it is not the "power law" data, please post that too.
- #45
naviakam
- 103
- 3
haruspex said:
This data and many others fit well with power law without any curve at the end.
However what I want to know is that if we have power law and exponential equations (as stated in post #39) how we can assign a potential function to them? This is what we need to present to the class! Please help on this.
Thanks
- #46
- 42,783
- 10,488
Do you mean a power law or a polynomial?naviakam said:
As I keep telling you, I don't even understand that question. Presumably you do have some idea of how a potential function would lead to an intensity versus voltage function, so give me an example. Pick some arbitrary potential function and show what I=f(V) it would lead to.naviakam said:
- #47
naviakam
- 103
- 3
haruspex said:
If we have ##Y=KX^{-n}## where Y is number of particles and X is their energy.
Then we have a potential like ##V=CI^{4}## where V is the potential, C is a constant and I is the current.
The potential lead to the particles to be accelerated!
How this two equations could be related mathematically?
- #48
- 42,783
- 10,488
What current is this? Is it the current carried by the flow of ions?naviakam said:
If so, seems to me that you are not looking for a "potential function" but rather two functions of potential: how the current (rate of ions) and the energy per ion depend on an applied potential.
I.e. I=I(V) and E=E(V) lead to an observed relationship between I and E, and you want to find out what I(V) and E(V) are.
Am I close?
- #49
naviakam
- 103
- 3
haruspex said:
Yes you are right, then how it is formulated mathematically?
- #50
- 42,783
- 10,488
There is clearly no unambiguous way to extract two relationships from the one, but an obvious guess is that in a vacuum the energy would be directly proportional to the voltage, leaving you with a simple way to extract the relationship between voltage and current from the observed data.naviakam said:
But you got different results at some other pressure, so this is not a vacuum. Presumably the gas present saps some of the KE, but should not affect the current.
- #51
naviakam
- 103
- 3
Not sure how to calculate I(V) and E(V).haruspex said:
##E=ItV, V=CI^{4}, Q=KC^{-n}, Y=KE^{-n}##
Then
##Y=Q(I^5tV)^{-n}##
resulted in
##V=(QY)^{-n}(I^5t)^{-1/n}##
where t is the time, E energy, Y intensity, V potential, Q constant, I current.
If correct how it is written more in the math style?
What if the equation in post #39 is considered, how rewritten considering such potential?
Last edited:
- #52
- 42,783
- 10,488
Isn't E here the energy of an individual ion?naviakam said:
But I am worried about my earlier interpretation. Your data say the current (ions per unit time) and energy (per ion) are negatively correlated. I cannot imagine what physical set up would lead to that. An applied potential that increases one should increase the other, no?
Is it possible for you to provide a far more detailed description of the apparatus? What is being varied to get the different readings?
- #53
- 42,783
- 10,488
I assume the two columns in the data you posted are respectively x, y.naviakam said:
I just tried plotting y against x-4. Nothing like a straight line.
Please post exactly what power law equation (constants included) you get for the relationship.
- #54
naviakam
- 103
- 3
It is a plasma device called plasma focus consisting a chamber and electrode assembly of anode at the center and cathode around it. capacitor discharge (10 KV) in the gas filled the chamber accelerates the ions to MeV with the spectrum I sent the data earlier. The intensity of low energy ions are high and decreases with energy by ##E^{-n}## where n is around 4.haruspex said:
Last edited:
- #55
naviakam
- 103
- 3
This is another plot with power law fit in origin for the same device:haruspex said:
##Y=KX^{-n}## where ##K=6.8*10^{23}## and ##n=4.56##
- #56
- 42,783
- 10,488
I need the raw data and the power law equation you believe fits it for the same data.naviakam said:
The fit above doesn't look that great to me.
- #57
naviakam
- 103
- 3
power law was mentioned above and the data is:haruspex said:
1106.16 1.20E+10
1048.02 1.19E+10
994.96 1.27E+10
946.43 1.48E+10
901.95 1.92E+10
861.07 2.17E+10
823.44 2.79E+10
788.72 3.35E+10
756.65 4.31E+10
726.96 5.83E+10
699.44 7.19E+10
673.89 8.53E+10
650.14 9.91E+10
628.04 1.17E+11
607.45 1.32E+11
588.24 1.54E+11
570.31 1.79E+11
553.55 2.07E+11
537.87 2.30E+11
523.20 2.74E+11
509.46 3.13E+11
496.58 3.45E+11
484.51 3.91E+11
473.18 4.23E+11
462.54 4.83E+11
452.56 4.94E+11
- #58
- 42,783
- 10,488
Is this the data that goes with the equation in post #55?naviakam said:
- #59
naviakam
- 103
- 3
Yes.haruspex said:
- #60
naviakam
- 103
- 3
##Y=P(p)Y1(E)+(1−P(p))Y2(E)##, where P(6mbar)=0 and P(10mbar)=1.
How to calculate Y(V) and E(V)?
Potential is ##V=YE/It##.
where t is the time, E energy, Y intensity, V potential, I current.
How to calculate Y(V) and E(V)?
Potential is ##V=YE/It##.
where t is the time, E energy, Y intensity, V potential, I current.
Last edited:
Similar threads
- · Replies 3 ·
- · Replies 7 ·
- · Replies 2 ·
- · Replies 26 ·
- · Replies 4 ·
- · Replies 1 ·
- · Replies 1 ·