exis
- 22
- 0
Homework Statement
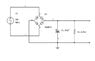
A 50V peak AC signal at 50Hz is fed to a 1:1 turns ratio transformer full-wave rectifier circuit. The full-wave rectifier waveform is smoothed by the use of a capacitor C=47uF, R=4.3kohms.
I need to calculate the peak diode current (however before this i was asked to calculate the average voltage across the load resistor R and the peak-peak rippe voltage across R)
The Attempt at a Solution
Vrippe(peak-peak) = Vpeak/(2fRC) = 50/(2*50*4300*47*10^-6) = 2.47V
Vdc = Vpeak - Vripple(peak-peak)/2 = 50 - 2.47/2 = 48.76V
I reasoned that the maximum current through the diode occurs when Vin=Vpeak. Therefore I_max=Vpeak/R=50/4300=11.6mA.
I tried considering the current through the capacitor as well but didnt know how to find the max current through it.